Informal Limits

Return to Course Outline

Previous Lecture

Misc

Problem Set 1

The problem set deals with material we’ll read and discuss between yesterday and next Wednesday -- so you can start doing some pieces of it now, but don’t expect to be able to do the whole thing yet.

Note the 2 due dates, one for completing it and one for grading it.

• You should be finished by the end of the day on the “Complete By” date; any time after that I may assign the next problem set, and I won’t be sympathetic if you wait ’til after that date to set up a grading meeting and then discover that there are no times left.
• Come meet with me to discuss your solution before 5:00 PM on the “Grade By” date. These meetings can be any time before then, they don’t have to be on the 12th.

You do not have to give me a copy of your solution until you bring it to your grading meeting.

Demonstration of how to make appointments with me via Google calendar.

Questions?

Limits

The “Intuitive Definition of a Limit” part of Section 2.2

Inituition and muPad

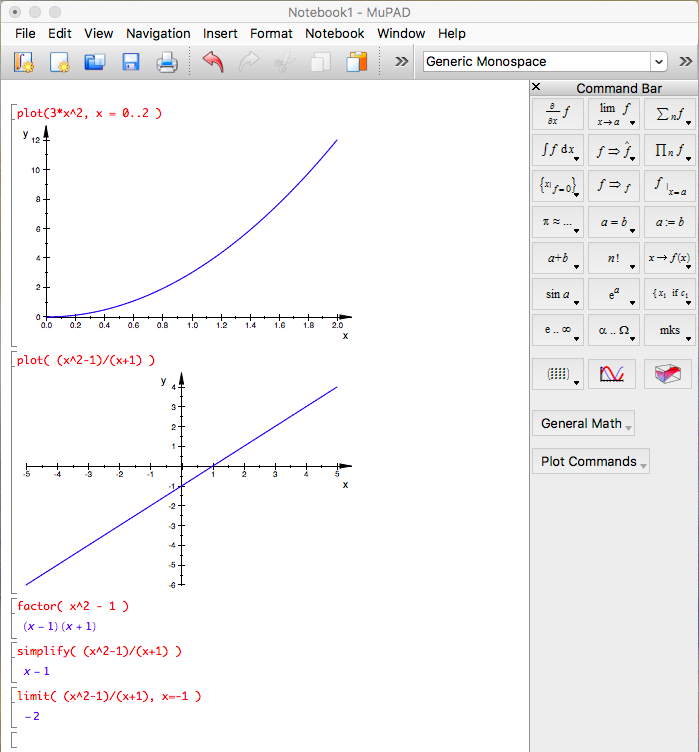
Problem. Guess lim_x→1 3x².

Method 1: A table of function values for x values approaching 1.

Method 2: graph the function (done via muPad, see below).

Problem. Guess lim_x→-1 (x²-1)/(x+1).

Tabulating some function values suggests the limit is -2.

This is also consistent with a graph (via muPad).

And with what muPad finds:

Summary. A function’s limit as x approaches some constant a is the single value (if any) the function gets closer and closer to as x gets closer and closer to a. Tables and/or graphs can often help you see intuitively what such a limit must be.

Algebraic Techniques

Often functions are undefined because they require calculations such as 0/0, 0 × ∞, etc.

You can sometimes algebraically rewrite the function to eliminate these problems.

Example. Rewrite (x²-1)/(x+1) into something that makes it easier to see why lim_x→-1 (x²-1)/(x+1) = -2.

(x²-1) is a difference of squares, and therefore factors into (x+1)(x-1). The (x+1) cancels the (x+1) in the denominator of our function, leaving just (x-1). Evaluating x - 1 at x = -1 gives -2, consistent with the limit we guessed above.

See the muPad example above for how muPad can do some of the algebraic manipulations (or, for that matter, find the limit in one fell swoop).

Summary. Algebraic simplification is a common tool (and our first) for being able to reason a little more rigorously than just guessing about limits.

Next

Limit laws and algebra.

Read section 2.3 until the phrase “one-sided limits” appears (roughly half way through subsection “Additional Limit Evaluation Techniques”). Stop there.

Next Lecture