SUNY Geneseo Department of Computer Science

Drawing Polygons with Holes

Return to List of Lectures

Misc

CIT has student jobs for a database programmer and a Web assistant for fall 2013

• Contact Paul Jackson (jackson@geneseo.edu) if interested

Exam 2 is Thursday (April 11)

• Material since 1st exam (e.g., dynamic programming, shortest-path algorithms, greedy algorithms, minimum spanning trees)
• Rules and format otherwise similar to 1st exam, esp. open-references rules

Questions?

Third question on minimum spanning tree problem set (divide-and-conquer algorithm): Just prove or disprove the claim that the given method finds minimum spanning trees, you don’t have to write out the algorithm

Second question: summarize class discussion for why Prim’s algorithm doesn’t need modification, and then find an answer re Kruskal’s

A Greedy Approach to Drawing Holes

Problem: draw a polygon with a hole by filling the space outside the hole with triangles without any triangle overlapping the hole

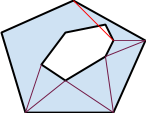
• Assume both polygons are convex
• Polygons may have large numbers of vertices (10s) in order to look like smooth curves

Set up the problem by numbering the vertices around the hole and rim of the polygon.

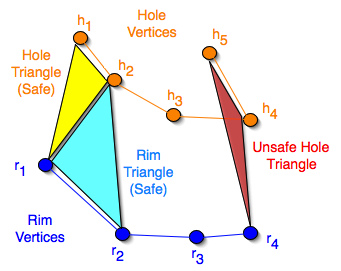
• There are n vertices around the hole, and m around the rim
• Triangles are either hole triangles or rim triangles, according to whether they have an edge on the hole or the rim (I don’t try to build any triangles that aren’t one or the other of these types)
• Triangles are either safe or unsafe, according to whether they overlap the hole or not
  • Hole triangle (h_i, r_j, h_i+1) is safe iff r_j is on the rim-ward side of line (h_i,h_i+1)
  • Rim triangle (r_j, h_i, r_j+1) safe iff r_j and r_j+1 are rim-ward of either line (h_i-1,h_i) or line (h_i,h_i+1)

Instinct is for a triangulation algorithm to loop through both sets of vertices simultaneously, adding either a hole or rim triangle to a growing set of triangles according to which kind is locally safe; arbitrarily add either if both triangles are safe.

• This strategy is greedy in the sense that it grabs a locally acceptable triangle to add to the list without worrying about whether doing so might preclude finding a safe triangle somewhere later, when a different earlier choice might have allowed one
• A pair of theorems that would justify using this strategy
  • Theorem 1: if there is a safe triangulation of vertices (h_i, ... h_n) and (r_j, .., r_m), and rim triangle (r_j,h_i,r_j+1) is safe, then there is a safe triangulation of vertices (h_i, ... h_n) and (r_j+1, .., r_m)
  • Theorem 2: if there is a safe triangulation of vertices (h_i, ... h_n) and (r_j, .., r_m), and hole triangle (h_i,r_j,h_i+1) is safe, then there is a safe triangulation of vertices (h_i+1, ... h_n) and (r_j, .., r_m)
• Prove theorem 2

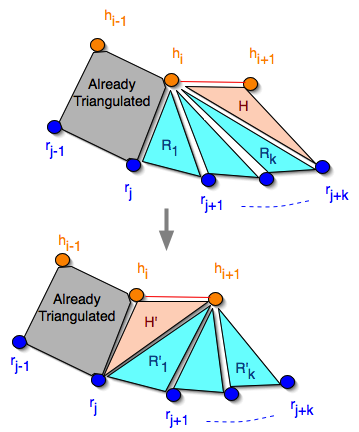
• We’re given that there is a sequence, S, of safe triangles from vertices h_i and r_j. It must eventually have a triangle with the h_i to h_i+1 edge, i.e., a hole triangle. The safe sequence might have some rim triangles R₁, … R_k before the hole triangle, possibly with k = 0, so in general the hole triangle is (h_i, r_j+k,h_i+1). Since this triangle must be safe, and the hole triangle (h_i,r_j,h_i+1) is also assumed to be safe, and the polygon is convex, all the vertices r_j through r_j+k are on the rim-ward side of line (h_i,h_i+1). Therefore the hole triangle (h_i,r_j,h_i+1) can be followed by rim triangles R'₁, …, R'_k , which are all safe, to “rejoin” the safe sequence S at h_i+1 and r_j+k, giving a safe triangulation of vertices (h_i+1, …, h_n) and (r_j, …, r_m).
• Interestingly, because of the asymmetry between what makes a hole triangle safe and a rim triangle safe, it’s not so clear that theorem 1 is true, although a similar argument plus more reliance on convexity might prove it.
• But even theorem 2 alone provides a correct algorithm, namely one that greedily uses a hole triangle if it can, and a rim triangle only if it is the only choice.

Next

Thursday: hour exam

Tuesday (4/16): GREAT Day, no class (so you can give/hear presentations)

April 18: Introduction to backtracking (not in book)