SUNY Geneseo Department of Computer Science

Minimum Spanning Trees

Return to List of Lectures

Misc

Exam 2 is next Thursday (April 11)

• Material since 1st exam (e.g., dynamic programming, shortest-path algorithms, greedy algorithms, minimum spanning trees)
• Rules and format otherwise similar to 1st exam, esp. open-references rules

Questions?

Minimum Spanning Trees

Example

• Build a minimum spanning tree via Kruskal’s algorithm
  • Book’s references to “Build_Set” etc. assume solutions to the so-called “Union-Find” problem are available as subroutines for Kruskal. Union-Find problem involves a group of disjoint sets, and 2 operations: find the set that a given element belongs to, and combine 2 sets into one via a union operation. Note that these are exactly the operations that Kruskal needs. Clever tree-based representations of sets allow logarithmic time union/find operations.

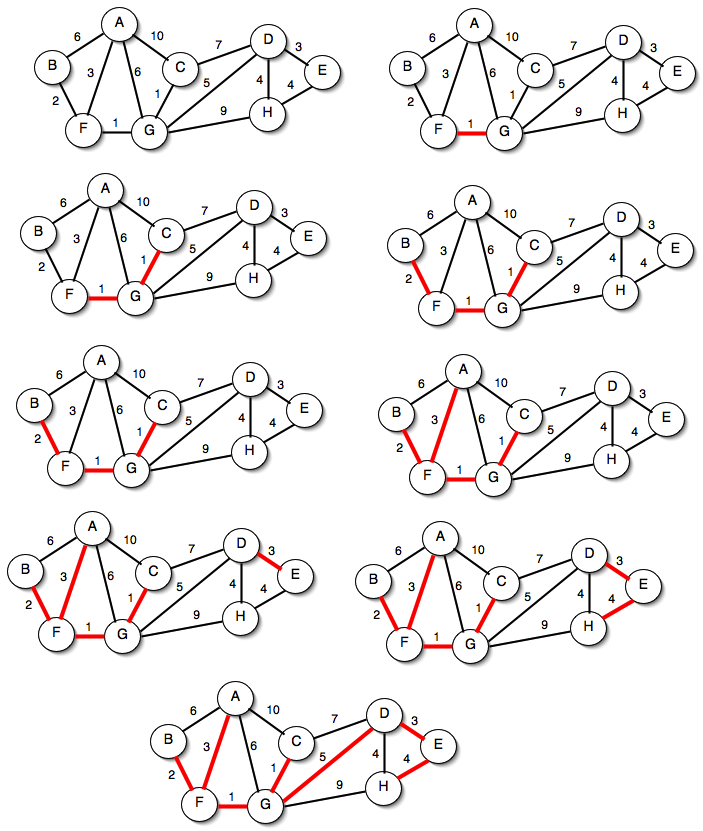
• Build a minimum spanning tree via Prim’s algorithm
  • Note that keys associated with vertices are minimum distances to the MST as it exists at the moment
  • Parent values are tentative, change as distance keys do. Parents become final when vertices are removed from priority queue.

• Note that this built a slightly different MST from Kruskal’s algorithm. This is simple a consequence of the fact that a graph generally has several minimum spanning trees, and the algorithms aren’t guaranteed to find any particular one.

Some observations/theorems about minimum spanning trees

• There are counter-examples to most claims you might guess about cycles (e.g., that the lightest edge in any cycle will be in every minimum spanning tree, that at least one edge from every cycle will be, etc.)
• If there is a unique lightest edge, (u,v), in a graph, then it is in every minimum spanning tree
  • Proof: Suppose for the sake of contradiction that Prim’s algorithm (which we know is correct) built an MST without the light edge. Then the key values for vertices u and v, and thus the weights of the edges attaching u and v to the MST, must be higher than the minimum weight. But now we can create a lower-cost spanning tree by inserting the minimum weight edge into the tree built by Prim, and removing some other edge to break the resulting cycle; this contradicts the minimality of the tree Prim built.
  • (A little cleaner version of this proof simply assumes that some MST exists that doesn’t use the minimum-weight edge, without saying where that MST comes from, and then proceeds as above with the observation that you can insert the minimum-weight edge and remove some other to get a better-than-minimal MST.)
• Somewhat unintuitively, it is not true that a unique highest-weight edge is never in a minimum spanning tree: that edge could be on the only path connecting some vertex to the rest of the graph.

Hand out minimum spanning tree problem set

Next

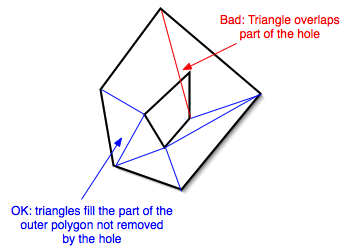
More greedy algorithms

Particularly one for drawing polygons with holes in computer graphics