Problem Set 12—Minimum Spanning Trees

Purpose

Background

Exercise

Solve each of the following problems.

Problem 1

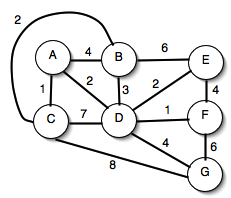
Show how each of Prim’s and Kruskal’s algorithms would find minimum spanning trees in the following graph. For Prim’s algorithm, assume that the starting vertex is vertex A.

Problem 2

Our textbook defines the minimum spanning tree problem for connected graphs. In an unconnected graph, one obviously can’t have a single minimum spanning tree, because being unconnected means that there are some vertices that are simply unreachable from others. However, one can have a minimum spanning forest, i.e., a set of minimum spanning trees, one for each connected component. Determine what, if any, modifications Prim’s and Kruskal’s algorithms would need in order to produce minimum spanning forests for unconnected undirected graphs. Give pseudocode for the resulting algorithms (unless no modification is needed, in which case the book already has adequate pseudocode).

Problem 3

Problem 23.2-8 in our textbook.

Follow-Up

I will grade this exercise in a face-to-face meeting with you. Please bring a written solution to your meeting. During the meeting, I will look over your solution, give you my reactions to it, answer any questions you have about it, etc.

Meetings should take about 15 minutes. Sign up either on the paper schedule outside my office or via Google calendar. If you work in a group, the entire group can schedule a single meeting with me. Be sure to have your grading appointment before the end of the day on the due date above.