SUNY Geneseo Department of Computer Science
The Floyd-Warshall Algorithm
Tuesday, March 26
CSci 242, Spring 2013
Prof. Doug Baldwin
Return to List of Lectures
Previous Lecture
Questions?
Floyd-Warshall Algorithm
Problem?
- Produce table of distances, D[i][j] = shortest distance from vertex i to vertex j
Carry it out
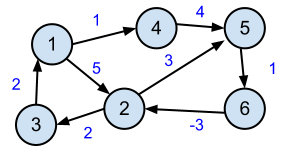
- As dynamic programming
- Based on progressively expanding the set of vertices considered as intermediates on shortest paths
- Recurrence basically says the shortest path involving intermediate vertices numbered through k+1 is either the shortest path involving vertices through k (i.e., vertex k+1 doesn’t shorten the best path seen so far), or it’s a shortest path from the source vertex to vertex k+1, and then from k+1 to the destination—and neither of those segments uses vertex k+1, since doing so would create a cycle.
- D0 = W (W is just initial adjacency matrix with edge weights)
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
0 |
5 |
∞ |
1 |
∞ |
∞ |
| 2 |
∞ |
0 |
2 |
∞ |
3 |
∞ |
| 3 |
2 |
∞ |
0 |
∞ |
∞ |
∞ |
| 4 |
∞ |
∞ |
∞ |
0 |
4 |
∞ |
| 5 |
∞ |
∞ |
∞ |
∞ |
0 |
1 |
| 6 |
∞ |
-3 |
∞ |
∞ |
∞ |
0 |
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
0 |
5 |
∞ |
1 |
∞ |
∞ |
| 2 |
∞ |
0 |
2 |
∞ |
3 |
∞ |
| 3 |
2 |
7 |
0 |
3 |
∞ |
∞ |
| 4 |
∞ |
∞ |
∞ |
0 |
4 |
∞ |
| 5 |
∞ |
∞ |
∞ |
∞ |
0 |
1 |
| 6 |
∞ |
-3 |
∞ |
∞ |
∞ |
0 |
- Note as a shortcut that whenever dik = ∞, the ith row of Dk is the same as the ith row of Dk-1
- D2
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
0 |
5 |
7 |
1 |
8 |
∞ |
| 2 |
∞ |
0 |
2 |
∞ |
3 |
∞ |
| 3 |
2 |
7 |
0 |
3 |
8 |
∞ |
| 4 |
∞ |
∞ |
∞ |
0 |
4 |
∞ |
| 5 |
∞ |
∞ |
∞ |
∞ |
0 |
1 |
| 6 |
∞ |
-3 |
-1 |
∞ |
0 |
0 |
- Very important invariant: the kth row and column of Dk are unchanged from Dk-1
- Problem set asks you to explain why this must be
- This invariant means that actual implementations of this algorithm can use a single 2D array, not a 3D one, and update it in place without worrying about over-writing a value that will be needed in the future
- D3 (just the parts that we now know easy shortcuts for)
| |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
0 |
|
7 |
|
|
|
| 2 |
|
0 |
2 |
|
|
|
| 3 |
2 |
7 |
0 |
3 |
8 |
∞ |
| 4 |
∞ |
∞ |
∞ |
0 |
4 |
∞ |
| 5 |
∞ |
∞ |
∞ |
∞ |
0 |
1 |
| 6 |
|
|
-1 |
|
|
0 |
Hand out Floyd-Warshall problem set
Next
Another approach to shortest paths
Chapter 24 introduction + Section 24.3
- Pages 643 - middle of 650, 658 - 662
Next Lecture

