SUNY Geneseo Department of Computer Science

Dijkstra’s Algorithm

Return to List of Lectures

Questions?

Dijkstra’s Algorithm

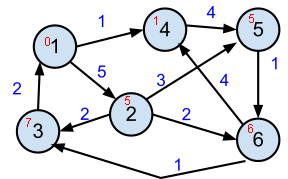
Carry it out (below is the graph used and final shortest path distances found—but not the steps through which they were found)

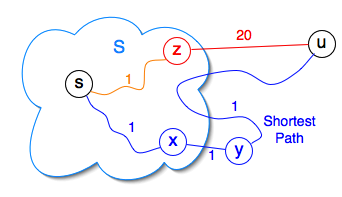
Is it always the case that every vertex u reachable from s (except s) that is added to S is adjacent to some vertex already in S at the time u is added?

• “Cooke’s Theorem”: u has a finite d only if u adjacent to some v in S
• Proof: d values decrease only through relaxation which only happens when an adjacent vertex is added to S
• But: what if Dijkstra doesn’t find finite d for some vertices reachable from s?

If every u added to S is adjacent to some vertex in S, does that fact lead to a simpler correctness proof for Dijkstra’s algorithm?

• If vertex in S adjacent to u is on shortest path to u, then convergence implies that u.d is correct when u added to S
• But could the adjacent vertex guaranteed by Cooke’s Theorem not be on the shortest path?

Finish this analysis for extra credit (up to 1/2 problem set)

• i.e., Plug the hole in the proof of Cooke’s Theorem (or show that the theorem doesn’t hold because the hole can’t be plugged), and prove that some vertex adjacent to u and in S is on a shortest path when u is added to S (or show that this isn’t always true)

Hand out Dijkstra problem set

Next

Greedy algorithms

(Dijkstra’s algorithm is a greedy algorithm)

Sections 16.1 and 16.2