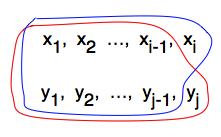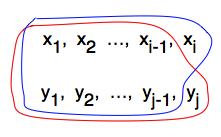SUNY Geneseo Department of Computer Science

Sequence Comparisons via Dynamic Programming

Return to List of Lectures

Questions?

Problem 1 in problem set?

• Think of the choices Stacey has about what to do with the kth course
• She can take it, in which case she has c_k more credits but p_k fewer dollars to spend on the other courses
• Or she can not take it, in which case all her credits come from other courses, and all her money goes to take them
• She should make whichever of these choices leads to the most credits
• So the recurrence for her maximum number of credits for courses 1 through k and m dollars is
  • maxCredits( k, m ) = max( c_k + maxCredits(k-1,m-p_k), maxCredits(k-1,m) )
  • maxCredits( 0, m ) = 0

Sequence Matching by Dynamic Programming

Biological application: how similar are 2 DNA sequences or proteins

Longest common subsequence

• Section 15.4
• A G T matches A C C C C G C T and T A A G T C
• C(i,j) = length of longest common subsequence of X_1..i and Y_1..j
  • = 0 if i = 0 or j = 0
  • = C(i-1,j-1) + 1 if i, j > 0 and X_i = Y_j
  • = max( C(i-1,j), C(i,j-1) if i, j > 0 and X_i ≠ Y_j
• Reflects two ways to find a longest common subsequence when you can’t automatically stick the last element of X and Y at the end

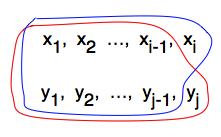
Needleman-Wunsch algorithm

• DNA sequences X = x₁, x₂, …, x_n and Y = y₁, y₂, …, y_m where x_i, y_i come from {A,C,G,T}
• Want to match X and Y so “similar” bases match, possibly by inserting gaps

• Similarity measured by function S(a,b) for a, b in {A,C,G,T} and gap penalty d
• Maximize sum over pairs in final alignment of S(a,b) where alignment pairs a and b and d where alignment inserts a gap in either sequence
• Element i of X and element j of Y can be paired at cost S(x_i,y_j), or either can be paired with a gap in the other sequence, leaving all i (or j) elements of that other sequence to align with the remaining elements in this sequence
• Recurrence for C(i,j) = maximum similarity score for aligning X_1..i with Y_1..j
  • C(i,0) = d×i
  • C(0,j) = d×j
  • C(i,j) = max( S(X_i,Y_j) + C(i-1,j-1), d + max( C(i-1,j), C(i,j-1) ) )
• Code for an iterative version

        score( X, Y, n, m )
            let C[0..n,0..m] be a new table
                // C[i,j] = max score aligning X1..i w/ Y1..j
            for i = 0 to n
                C[i,0] = d * i
            for j = 0 to m
                C[0,j] = d * j
            for i = 1 to n
                for j = 1 to m
                    C[i,j] = max( S(Xi,Yj)+C[i-1,j-1], d + C[i-1,j], d + C[i,j-1] )
            return C[n,m]

Next

Shortest paths in graphs

Section 25.2 through “Constructing a shortest path”

• Top of page 693 through first 1/3 of 697