SUNY Geneseo Department of Computer Science

Introduction to Graphs

Return to List of Lectures

Questions?

Graphs are data structures like stacks or queues, but more so than stacks and queues, they are also overtly mathematical abstractions, and as such have uses in modeling lots of phenomena and relationships without necessarily intending software implementations of those models.

Diagram conventions: edges are lines, vertices are circles.

Graphs

Trees vs graphs

• A is the parent of B—represent by a directed edge from vertex A to vertex B (edges are directed because parent-child relationship isn’t symmetric, but you could choose either direction, as long as you choose one and use it consistently)
  • Example

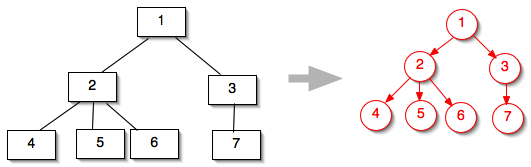
• To a graph theorist, any undirected graph with certain properties is a tree, and any tree is a graph, for example

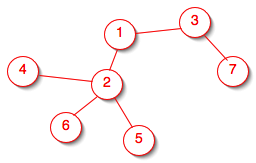
• You can also have directed trees with roots (in an undirected tree there is no unique root)
• Trees are acyclic and connected
• Which is equivalent to every pair of vertices has unique simple path
  • Proof (that acyclic and connected implies unique simple path): Suppose there were multiple paths, then at some point on the way from vertex A to vertex B there would be a choice of path, and at some other point before B the choices would reconverge. The paths between the last choice and first convergence form a cycle, which is a contradiction. (So this was formally a proof by contradiction)
• See appendix B5 for more

Graph example based on foods people like

• People’s foods
  • Prof. Baldwin: chocolate, pizza, mac & cheese
  • Yong: Choc., m&c, pizza, PBJ
  • Sean: Chicken Parm, PBJ sandwich, grilled cheese
  • Eli: tacos, stir fry
• One representation is as a bipartite graph. Here the two kinds of vertex are people and foods, and directed edges mean that a person likes a food.

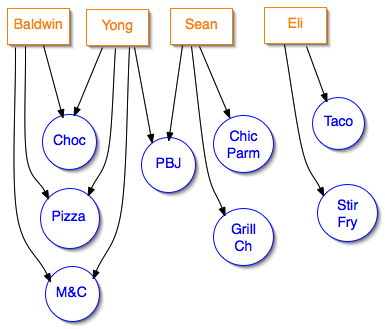
• You could also consider a representation in which vertices are foods, and an undirected edge between two vertices means that both are liked by some person (there doesn’t have to be just one way of representing something as a graph)
  • Technical problem: to record which person likes two foods you would have to have multiple edges between some pairs of vertices, which isn’t allowed by the definition of “graph.”
  • Could resolve this by realizing that what you have is really multiple graphs on the same vertex set
  • Or pragmatically, edges could carry auxiliary information noting who likes the foods

Hand out graph problem set

Next

Breadth first search

Read Section 22.2