- Exam 1
- Scheduled for next Wednesday (Feb. 17)
- Covers material on finite automata and regular languages
- Might logically fit better on Monday, Feb. 15
- Which do you prefer? Wednesday!
- “Flatland” movie
- This afternoon (Feb. 10), 2:30, Newton 201
- Set of postfix/prefix expressions
- Postfix: operators after operands
- Use 1-digit numbers and +, - operators
- So 12+ means 1+2 = 3
- 12+7- means (1+2) - 7
- Need to “balance” digits and operators, so same ideas as for balanced parentheses
- Maybe set up x = 1st operand, y = 2nd operand & operator
- Beware! This can be pumped to produce more valid postfix expressions, but you want to show that some valid string can be pumped into an invalid one, and you don’t generally have enough control to pick x and y this specifically
- Another idea: n operands require n-1 operators
- So let s = 1p+p-1
- y in first p symbols implies y is only 1s
- So xynz has too many operands (if n>1) for its operators
- Postfix: operators after operands
- Set of infix arithmetic expressions w/o parentheses or precedence
- e.g., 1+2-4, 7-2
- Maybe these must be non-regular because they can be transformed into postfix
expressions, which we know are non-regular?
- Neat hint at “reduction,” a technique for reasoning about one problem by transforming it into another
- But it doesn’t apply here
- Infix expressions without parentheses are actually regular, they’re
recognized by an NFA:

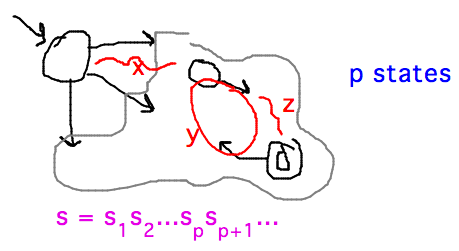
- Where do strings x, y, and z in pumping lemma come from?
- Parts of long string s that take DFA to a cycle of states, around that cycle,
and from it to an accepting state
- Parts of long string s that take DFA to a cycle of states, around that cycle,
and from it to an accepting state
- More pumping examples, particularly focused on “real” languages and broad capabilities of finite automata
- Also using closure properties of the regular languages to prove non-regularity