Cartesian Products of Sets

Return to Course Outline

Previous Lecture

Misc

Proofs Sessions in MLC

Mondays 3:00 - 4:00, Tuesdays 4:00 - 5:00.

Questions?

Formal proofs on problem set 7:

• Q1 (intervals). Informal.
• Q2 (number of subsets). Informal.
• Q3, Q4 (subset & union, real numbers). Formal.

Cartesian Product

Section 5.4.

The Concept

Suppose A = { red, green, blue } and B = { 0, 1 }. Then A × B = ...

{ (red,0), (red,1), (green,0), (green,1), (blue,0), (blue,1) }

How about B × B? B × B = { (0,0), (0,1), (1,0), (1,1) }

Imagine a 2-dimensional grid whose grid points have a natural number as their first coordinate and an integer as their second.

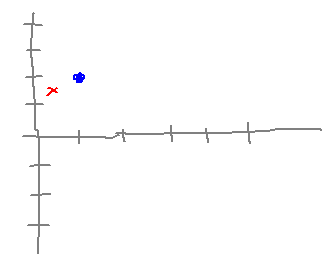
As a Cartesian product, this grid is ℕ × ℤ.

Using set-builder notation, the following portion of the grid...

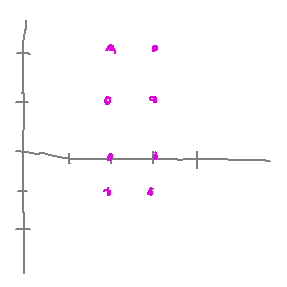
...is { x ∈ ℕ | 2 ≤ x ≤ 3 } × { y ∈ ℤ | -1 ≤ y ≤ 2 } or { (x,y) | x ∈ ℕ and 2 ≤ x ≤ 3 and y ∈ ℤ and -1 ≤ y ≤ 2 }.

Proofs

Prove part 3 of Theorem 5.25 — that (A ∩ B) × C = (A×C) ∩ (B×C)

Proof idea:

Prove each is a subset of the other

Show that (A ∩ B) × C ⊆ (A×C) ∩ (B×C): Let u = (x,y) be in (A ∩ B) × C. x is therefore in A ∩ B and y in C. This means x is in A and x is in B. Therefore (x,y) is in A×C and in B×C, i.e., u is in (A×C) ∩ (B×C).

Show (A×C) ∩ (B×C) ⊆ (A ∩ B) × C. Let v = (x,y) be in (A×C) ∩ (B×C). Therefore v is in A×C and v is in B×C. This means x is in A and y is in C, but also that x is in B. If x is in A and x is in B, then x is in A ∩ B. Thus v is in (A ∩ B) × C.

Here is a full formal version of this proof, with LaTeX source here.

Extending the Idea

If A, B, and C are sets, does it make sense to talk about A × B × C? What about ℝ³? What would those notations mean?

These do make sense.

By convention, A × B × C = { (a,b,c) | a ∈ A and b ∈ B and c ∈ C }

Although notice that a more literal application of the definition of Cartesian product would have A × B × C = { ((a,b),c) | a ∈ A and b ∈ B and c ∈ C } or { (a,(b,c)) | a ∈ A and b ∈ B and c ∈ C }. We’d probably need parentheses to emphasize the order in which to do the Cartesian products, i.e., (A × B) × C or A × (B × C). But as indicated above, this literal interpretation is set aside in favor of the simpler and more useful interpretation of A × B × C as a set of ordered triples.

Key Ideas

The concept of Cartesian product and its definition.

Using the choose-an-element method with Cartesian product in proofs. The “element” has parts that usually play a big role in the proof.

Next

Sets of sets, aka indexed families of sets.

Read section 5.5.

Next Lecture