SUNY Geneseo Department of Mathematics
Friday, March 15
Math 239 01
Spring 2019
Prof. Doug Baldwin
Section 4.2.
Prove that for all integers n ≥ 6, Fn ≥ (√2)n.
The first few Fibonacci numbers:
Proof outline:
Assume n ≥ 6.
Basis step 1, n = 6. F6 = 8 = (√2)6.
Basis step 2, n = 7. F7 = 13 ≥ √2 8 = (√2)7.
Induction case. Assume Fi ≥ (√2)i for all i in {6, 7, ..., k} for some k ≥ 7, and show that Fk+1 ≥ (√2)k+1 .
Fk+1= Fk-1 + Fk ≥ 2 Fk-1 ≥ 2(√2)k-1 = (√2)2 (√2)k-1 = (√2)k+1.
What was different about this from previous induction proofs we did?
This one started with n = 6. Starting somewhere besides 1 is Sundstrom’s “extended principle of induction,” and is quite common
This one also used “strong induction,” i.e. using an assumption about all values up to k, not just about k, in the induction step. Such assumptions often, though not always, require multiple basis steps.
To see what strong induction looks like formally, here’s a formal proof for this theorem, and it’s LaTeX source.
This is an example of (strong) induction applied to something very different from the usual proof subjects, namely arithmetic expressions. Because the induction is driven by the structure of the objects under consideration (i.e., expressions in this case), such applications are sometimes known as “structural inductions.”
Define an arithmetic expression to be either a single number (e.g., 17), or two expressions connected by an operator (+, -, ×, ÷).
Prove that every expression has 1 more number than it has operators.
e.g., 7 - 9 + 6, ((3+8)×(17-6))÷ 18
Proof outline:
The proof is by induction on the number of operators.
Basis step, an expression with no operators. Such an expression has must be just a number, and so has 1 number for 0 operators. 1 = 0 + 1.
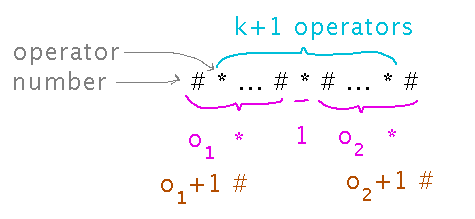
For the induction step, assume every expression with i operators, for i in {1,2,...k}, k ≥ 0, has i+1 numbers, and show that every expression with k+1 operators has k+2 numbers. Consider an expression with k+1 operators. Since k ≥ 0, there is at least 1 operator, so pick one and consider the expressions to its left and right. Let o1 and o2 be the number of operators in these expressions. The whole expression has o1 + o2 + 1 = k+1 operators. Both o1 and o2 are less than or equal to k, and so the left and right expressions have o1+1 and o2+1 numbers, respectively. Thus the total number of numbers in whole the expression is o1+1 + o2+1 = o1 + o2 + 2 = k+2.
Notice that this example also shows how strong induction doesn’t always need more than one basis case.
Introduction to set theory.
Read section 5.1.