Induction, Part 2

Return to Course Outline

Previous Lecture

Questions?

Proof by Induction

Section 4.1.

This style of induction, particularly using an induction step of the form P(k) implies P(k+1), is called “weak induction.”

Example

Progress check 4.3

Prove that for all natural numbers n, 1 + 2 + 3 + ... + n = n(n+1)/2.

There’s a non-inductive argument for this theorem that 1 plus the last element is n+1, as is 2 plus the 2nd to last, and 3 plus the 3rd to last, and so forth, for a total of n/2 pairs:

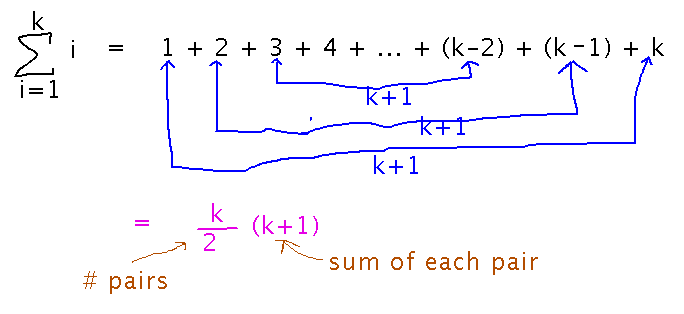
That phrase “and so forth” in this argument is a signal that the prover is assuming that some pattern continues indefinitely. That assumption may be wrong in subtle ways. Induction is a way to deal rigorously with “and so forths” in arguments.

We generally developed the proof in pieces as people saw them. In particular,...

• We quickly found a basis step of n = 1.
• If a theorem is phrased in terms of a natural number n, then it’s clearer to use some other variable, say k, for the value that implies P(k+1) is true in the induction step.
• For the induction step, we realized (as is common in inductive proofs about sums) that the sum to k+1 can be written as the sum to k (to which the induction hypothesis applies) plus one more term.
• Despite our textbook’s references to a predicate P in induction proofs, actual proofs may be clearer with more specific wording for references to the claim being proven.
• Induction proofs have a stylized structure (introduction, basis step, induction step, conclusion), with stylized wording for guiding readers through that structure.

Here is the proof that finally emerged from our discussions, and the LaTeX source file that generated it.

Next

Extending induction.

Start reading section 4.2.

Next Lecture