SUNY Geneseo Department of Mathematics
Wednesday, March 6
Math 239 01
Spring 2019
Prof. Doug Baldwin
A couple of LaTeX features in my proofs from last class...
cases environment for writing nice-looking piecewise definitionslabel and ref commands for cross-referencesSection 3.5.
Guess the missing digit from a UPC barcode.
For example (cryptically)...
This is an example of a “checksum,” a scheme for detecting errors in numeric codes based on sums of the numbers. In this case, the checksum is to ensure that scanners (or people typing product codes by hand) don’t mis-read or mis-type a digit.
For product codes, the scheme is: add up all the digits in odd-numbered positions (the 1st, 3rd, etc.) and multiply by 3. Add all the digits in even-numbered positions and add the sum to the previous product. The total should be congruent to 0 mod 10.
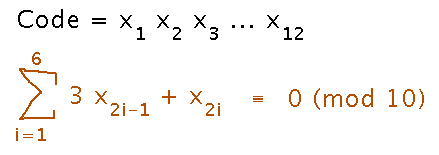
If a digit is missing, as in our example, you can find a value for it that makes the above congruence hold. If you have all the digits but the congruence doesn’t hold, you know that at least one digit is wrong.
Try it on your own product codes.
If the missing digit is in an even position, it’s pretty easy to calculate a unique value for it. But what if the missing digit is in an odd position? It’s fairly easy to calculate what 3 times the missing digit is (mod 10), but are you sure there’s a unique digit that can be multiplied by 3 to produce that value?
Theorem: For all integers x, if 0 ≤ x ≤ 9, then there is a unique integer y, 0 ≤ y < 10, such that 3x ≡ y (mod 10).
Proof: The proof idea is to simply check what 3 times each number from 0 to 9 is mod 10, and that each possible result between 0 and 9 appears exactly once.
This is essentially a proof by cases (10 of them), suggesting how modular congruence can give rise to proofs by cases. Usually you’d hope to work with a modulus smaller than 10, so that there were fewer cases to check.
A real-world use of congruence.
Modular remainders can provide cases for proofs.
Introduction to induction.
Read the preview activities and the “Inductive Sets” subsection of section 4.1.