Geneseo Math 239 01 Compound Statements

Questions?

Compound Statements

Section 2.1.

The Basic Connectives

What would have to be the truth/falsehood of the statements “Math 239 is fun” and “The world has gone mad” in order for the following statements to be true?

If Math 239 is fun, then the world has gone mad. This is true except when Math 239 is fun but the world is not mad.
Math 239 is fun and the world has gone mad. Both “Math 239 is fun” and “The world has gone mad” must be true.
Math 239 is fun or the world has gone mad. Either (or both) of “Math 239 is fun” and “The world has gone mad” need to be true.
Math 239 is fun if and only if the world has gone mad. This is true if both parts are true or both are false.

Is “if and only if” the same as “exclusive or”? No, but there is a connection between them, as seen in their truth tables:

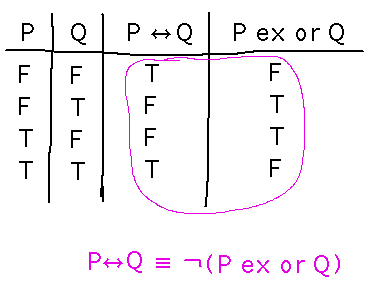
If-and-only-if and exclusive or have exactly opposite truth tables: iff is not ex-or

Is “P exclusive or Q” the same as “Q exclusive or P”? Let’s extend the truth tables and see:

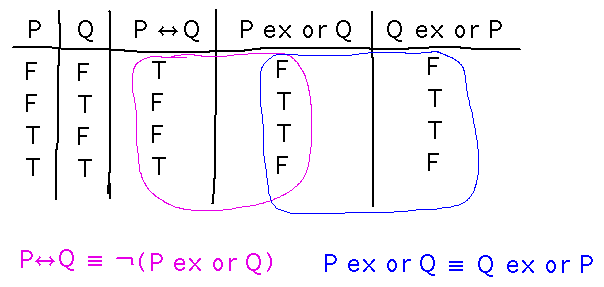
P exor Q and Q exor P have the same truth table

Now you have proven that exclusive or is commutative. Proofs in propositional logic are some of the few proofs that you can sometimes do just by listing all the possibilities. Truth tables are a legitimate core of those proofs.

Tautology/Contradiction and Truth Tables

Use truth tables to determine whether P → ¬ P is a contradiction, tautology, or neither.

How about P ↔ ¬ P?

While both of these sound horribly contradictory in English, only P ↔ ¬ P is a contradiction in the technical sense:

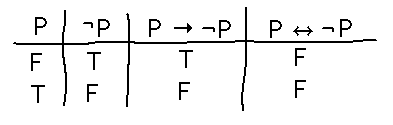
P implies not P is true when P is false and false when P is true; P iff not P is always false

Beware of notation: the logical connectives all have operator symbols that you haven’t necessarily seen before:

and: ∧
or: ∨
if: →
if and only if: ↔

Tables in LaTeX

The tabular environment produces tables with aligned rows and columns, rules, etc.

Here is an example .tex file and the resulting PDF that demonstrate a simple use of this environment.

Preview of Equivalence

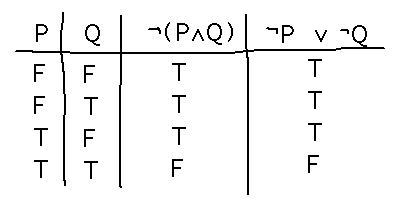
(Inspired by progress check 2.2.) which, if any, of the following are equivalent to ¬(P ∧ Q). Use a truth table to check:

(¬ P) ∧ (¬ Q)
(¬ P) ∨ (¬ Q)
¬ (P∨ Q)

It turns out that it’s (¬ P) ∨ (¬ Q):

not (P and Q) is true except when P and Q are both true; so is (not P) or (not Q)

Problem Set

See handout for details.

Equivalence of logical statements.

Read section 2.2.