SUNY Geneseo Department of Mathematics

Function Composition

Monday, April 10

Math 239 01
Spring 2017
Prof. Doug Baldwin

Return to List of Lectures

Previous Lecture

Misc

Email Reading Summaries

Please just use plain text in the body of the email rather than attachments, etc.

Colloquium

“Quaternions and Number Systems”

Rob Stephens, visiting professor here

Thursday, April 13, 2:45 PM, Newton 203

Extra credit for write-ups, as usual.

Questions?

Function Composition

Section 6.4

Composing Special Functions

(Inspired by Progress Check 6.19).

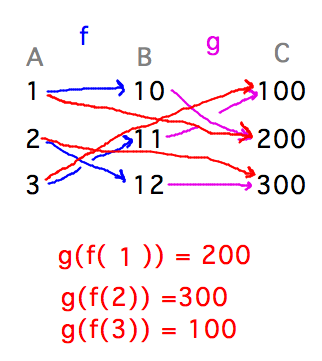
Let A = { 1, 2, 3 }, B = { 10, 11, 12 }, and C = { 100, 200, 300 }.

Draw arrow diagrams for an injection f : A → B, an injection g : B → C, and their composition.

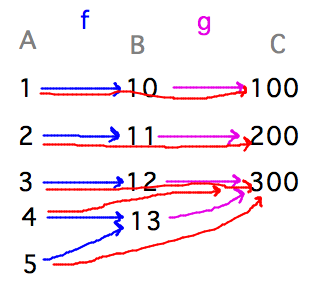
Draw arrow diagrams for a surjection f : A → B, a surjection g : B → C, and their composition (the sets involved in this example got redefined as we discussed the example, to make it more interesting — see below).

Relevant ideas or questions from the reading:

Definition of composition: If A, B, and C are non-empty sets, and f : A → B and g : B → C are functions, then g ○ f : A → C is a function defined by (g ○ f)(x) = g(f(x)). f is the inner function, g is the outer function.
There are also theorems relating whether a composition is an injection, surjection, etc. to whether f and/or g are. See the textbook for the specific theorems.

Solutions.

Injective functions:

1-to-1 arrows from A to B and B to C define 1-to-1 arrows from A to C

Surjective functions on sets A = {1,2,3,4,5}, B={10,11,12,13}, and C = {100,200,300}.

Surjections from A to B and B to C compose into surjection from A to C

Comments.

These examples provide concrete examples of what the definition of composition means.
They also illustrate theorems about how the properties of compositions relate to properties of the functions being composed.

Proofs about Compositions

For example, Theorem 6.20 part A (if f : A → B and g : B → C are both injections, then g ○ f is an injection).

Relevant ideas or questions from reading:

Definition of injection will help

Solutions.

Show that if (g○f)(a₁) = (g○f)(a₂) then a₁ = a₂.
(g○f)(a₁) = (g○f)(a₂) means g(f(a₁)) = g(f(a₂))
Since g is an injection, g(f(a₁)) = g(f(a₂)) means f(a₁) = f(a₂).
And since f is an injection, a₁ = a₂.
QED

Comments.

Proofs often take the definition of a property and apply it to g○f as the goal
Then work backward using the definition on g and then f

Summary Comments

I see two main ideas in this section.

The definition of composition
Ideas for proving things about properties of compositions.

Inverses of functions.

Read textbook section 6.5.

Next Lecture