Misc
Colloquia
Yu-Min Chung
- “Computational Topology with Applications in the Natural Sciences”
- Monday, Feb. 27, 2:30 PM, Newton 203
Eleni Panagiotou
- “Quantifying Entanglement in Physical Systems”
- Thursday, March 2, 2:30 PM, Newton 203?
Both speakers are faculty candidates
Extra credit for writing a paragraph or so summarizing connections you make between either or both talks and your own interests.
Questions?
The Division Algorithm and Congruence
Section 3.5
The Division Algorithm
Reading ideas:
- Every integer a can be written as a = bq + r, i.e., q is the quotient and r the remainder
- For instance, for even and odd numbers (b = 2) r = 0 for even and 1 for odd
- Justifies the idea that integers are even and odd but never both
- Also expands the idea of separating integers into even and odd to more groups based on larger ranges of r
- This idea can also provide cases for proofs, based on the possible r values
- Reading gives rules for arithmetic in the presence of congruence
- Reading also discusses the reflexive, symmetric, and transitive properties of congruence
Examples: find r such that a = bq + r and 0 ≤ r < b for each of the following a and b pairs:
a = 13, b = 4: q = 3, r = 1, i.e., 13 = 4×3 + 1
a = 6, b = 8: q = 0, r = 6, i.e., 6 = 8×0 + 6
a = -5, b = 4: q = -2, r = 3, i.e., -5 = -2×4 + 3
- Or q = -1, r = -1, i.e., -5 = -1×4 - 1?
- But this decompostion violates the rule that 0 ≤ r < b
- Only the first decomposition (r = 3) is correct
The mod operator, e.g., 5 mod 3 = 2, finds r
Often convenient to talk about, but a bit informal. Formally, prefer 5 ≡ 2 (mod 3) over 5 mod 3 = 2.
Congruence
Radix-complement numbers. The basis for how computers and many other calculators represent negative numbers (i.e., as positive numbers that thanks to Theorem 3.28 “act like” the negative one relative to the fixed number of digits the computer or calculator can store).
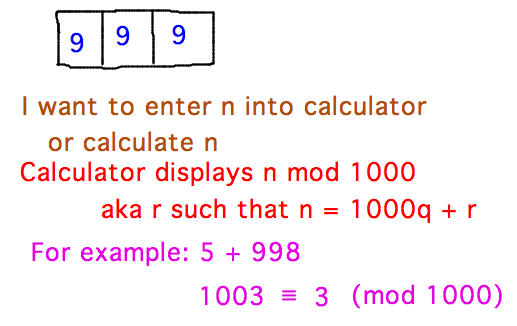
Electronic devices can use large positive numbers as negative, rather than needing a special representation for them.
This is justified by the following proposition: for all integers n and natural numbers B, -n ≡ (B-n) (mod B).
Proof: Assume n is an integer and B a natural number. Then (-n - (B-n)) = -n - B + n = -B = (-1)B. By the definition of congruence (a ≡ b (mod n) if and only if n divides (a-b)), -n is then congruent to (B-n) (mod B). QED
Next
Introduction to proof by induction
Read section 4.1