Induction Part 2

Return to List of Lectures

Previous Lecture

• Misc
  • GROW STEM (Geneseo Reaching Out to Women and Under-Represented Minorities in STEM) networking meeting
    • Thursday, Oct. 20 (tomorrow), 5:15 PM, Bailey 102
• Questions?
  • Extra credit conjectures: schedule 15 minutes to present them, that or more to discuss ideas
• Induction
  • Section 4.1
  • Prove that for all natural numbers n, every set with n elements has 2ⁿ distinct subsets
    • What is this saying? Examples?
      • { 1, 2 }, n = 2
      • Subsets: {1}, {2}, {1,2}, {}, 2² = 4
    • Proof
      • Induction!
      • Basis: n = 1, set is { a }
        • Subsets are {}, {a}, of which there are 2 = 2¹
      • Induction Step:
        • (If all sets of size k have 2^k subsets, then all sets of size k+1 have 2^k+1 subsets)
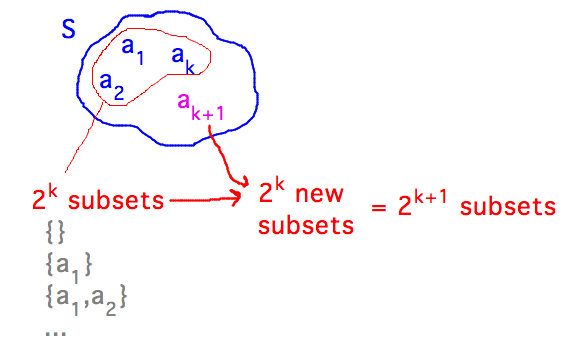
        • Let S be a set of k+1 elements
        • Think of S as consisting of k elements and one additional one
        • You can make 2^k subsets from the first k elements
        • From each of these subsets you can make another by adding element k+1
        • Each of these new subsets will be distinct from any of the first ones because it contains element k+1, and from all other subsets containing element k+1 because it contains whatever elements made the original subset distinct
        • The are no other subsets of S, because we constructed all the subsets that don’t contain element k+1, and the only other subsets are constructable by adding element k+1 to one of the subsets without it
        • The total number of subsets thus made is 2^k + 2^k = 2^k+1
          
      • See this proof written out formally, and the LaTeX file that produced it
• Next
  • Extensions to induction
  • Section 4.2

Next Lecture