Questions?
Newton’s Method Example
The goal is to try carrying out some of the steps of Newton’s algorithm by hand, in order to get a sense for how it works and to get at least one test case for the code you’ll write in the lab.
To start, you need concrete values for the algorithm’s inputs: a function, an initial guess at an x where the function is 0, and a tolerance to use in deciding when to stop.
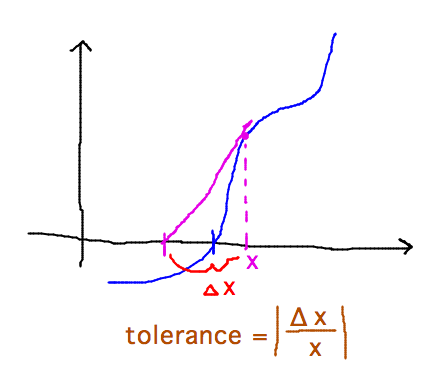
What is the tolerance?
- A value for the change in x during an iteration of the algorithm (Δx) as a fraction of the initial value of x in that iteration (i.e., Δx/x)
- When Δx/x falls below the tolerance, you’re willing to declare Newton to have converged on a zero of the function
First choice of inputs: f(x) = x2 - 8, initial x = 0, tolerance = 1
Note that f'(x) = 2x. Even though the algorithm as described in the video takes it as an input, we can calculate it as soon as we know f(x), and the function I describe in the lab handout does something similar, by using a helper “derivative” function to find f'(x) from f and x.
Also note that f(x) = 0 at x = ±√8
Try Newton’s method with these inputs
- Iteration 1: x becomes x - f(x) / f'(x) = 0 - -8/0
- Oops! Can’t divide by 0.
- This illustrates a problem that Newton’s method can face in real life: accidentally evaluating f and a place where its derivative is 0.
Second choice of inputs: f(x) = x2 - 8, initial x = 3, tolerance = 0.1
- Iteration 1: x becomes x - (f(x)/f'(x)) = 3 - 1/6 = 2 5/6
- Δx = 1/6, compare | Δx / (old) x | to tolerance: (1/6) / 3 = 1/18 < 0.1, done!
Even though this only did one iteration, the x value it ended up with, 2 5/6, aka 2.8333... in decimal, is quite close to the actual square root of 8: roughly 2.828.
Why does Newton’s method calculate x - f(x)/f'(x)? Basically because that’s where using the tangent to f(x) at x as an approximation to the function predicts that f(x) will equal 0. The derivation is based on the slope of the tangent and how far the tangent has to rise from 0 to reach f(x):
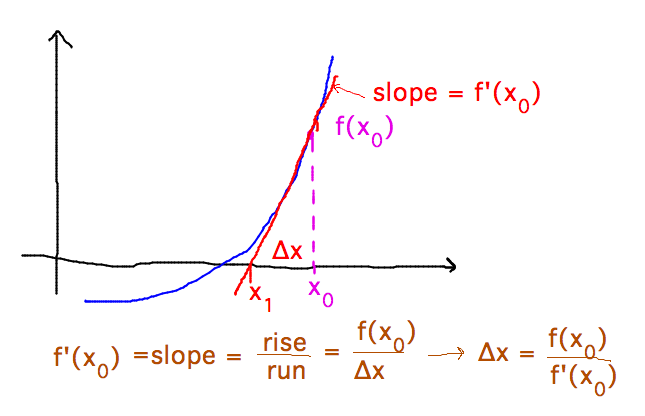
Also see the video for a version of this derivation.
Newton’s Method Lab
Next
Lab day for Newton’s method lab.
Modified complete-by and grade-by dates?
- Complete by Wednesday evening
- Grade by Friday