Plotting

Return to List of Lectures

Previous Lecture

Questions?

Terms related to functions?

“Call” a function: cause it to do its computation on a specific piece of data, e.g., y = f(6) in the command window or a script

“Define” a function: describe what it does, give it a name, etc., e.g., function [z] = f( wave ) .... end in a “.m” file

Plotting

Sections 6.2 and 6.3

Plot a function: plot the curve y = sinx + x between x = -2π and x = 2π.

Useful ideas from reading

• plot( ... ) plots a line
• You can then specify axis limits via axis( [ x1, x2, y1, y2 ] )
• You can label axes or title the graph with xlabel( 'label' ), ylabel(...), title(...)
• Change the plot style with a quoted string in plot, e.g., 'o' to plot points as circles
• Section 6.4 has lots in it, including...
  
  • A table with types of line graph
  • Ways to customize colors, point appearance, line style, etc.
  • What is the business with interactive plots via ginput?
    • See example below
  • How do you save a graph to file?
    • The easiest way is to use “Save As” from a figure window's “File” menu.
    • In the “Save As” dialog, you can pick from many different image file formats to save in.

How do you plot a function rather than a pair of vectors?

• Just fill the vectors with x and y values, much as we did in the vector lab.
• If the points are close enough together, the resulting plot will look like a smooth curve.

Should you do plotting in a script or in a function?

• You can do it in either place.

Here’s the code to plot y = sinx + x:

>> % plot sinx + x from -2pi to 2pi
>> x = -2*pi : pi/6 : 2*pi;
>> y1 = sin(x) + x;
>> figure(1)
>> plot( x, y1, 'r' )
>> axis( [ -2*pi, 2*pi, -10, 10 ] )

Now add in a plot of y = x² / 4 in a different color. A key idea is to use hold on to draw the new plot with the existing one, instead of replacing the existing one.

>> hold on
>> y2 = x.^2 / 4;
>> plot( x, y2, 'b' )
>> hold off

ginput records the positions at which you click your mouse, until you press the “Enter” key, at which point ginput returns vectors with the x and y coordinates of the clicks. Since ginput returns vectors of coordinates, you can plot them to track the path the mouse traced.

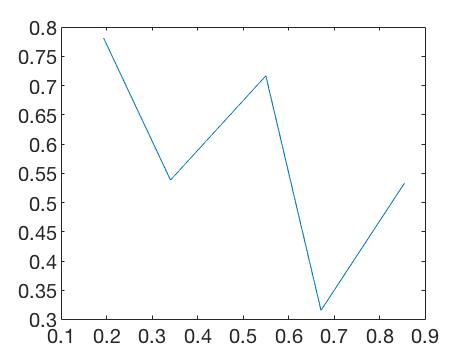
>> [clickX,clickY] = ginput()
clickX =
    0.1936
    0.3404
    0.5495
    0.6706
    0.8541
clickY =
    0.7809
    0.5384
    0.7166
    0.3156
    0.5334
>> plot(clickX,clickY)

This code produced this plot:



Lab 3: plotting parametric curves. See handout for details.

Next

Parametric curves

Watch this video introduction to, or review of, parametric curves if you aren’t familiar with them (or see it at https://www.youtube.com/watch?v=tsnHL1Lb5MU):

Next Lecture