- Programming club interest meeting
- Thursday (Feb. 25), 5:00 PM
- Bailey 101
- Exam 1 is tomorrow (Feb. 25)
- Material since start of semester (e.g., 3D coordinates and surfaces, vectors and their products, lines, planes, vector-valued functions, their derivatives, limits, integrals, arc length, muPad, etc.)
- Whole class period
- 4 - 6 short-answer questions
- Open references (book, notes, computer), closed person
- Can use calculators, CASes, etc.
- But tell me where you do
- Section 13.4
- T(s) = dr/ds; T(t) = v(t) / |v(t)|
- k = | dT/ds |
- Curvature = rate per unit length at which curve turns
- k = 1/|v(t)| | dT/dt |
- Principle unit normal vector (k ≠ 0)
- N = 1/k dT/ds
- = dT/dt / | dT/dt |
- Circle of curvature
- Tangent to curve at p
- Same curvature as curve at p
- Center lies on concave side of curve
- Radius of curvature at p = 1/k
- Example: do curves of the form y = x2n get more or less curved at x = 0
as n increases?
- Outline for answering: find curvature as function of n, then look at dk/dn
- Step 1: work out T(t)

- Step 2: Use quotient rule etc. to find dT/dt, then find its magnitude
- But notice that magitudes only need to be found numerically for t = 0, you can save a lot of work by doing this rather than finding symbolic magnitudes
- Start finding some derivatives we’ll need…
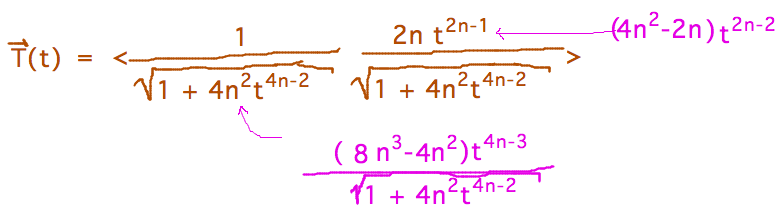
- …and class time runs out
- (After exam)
- Multivariable functions
- Read section 14.1