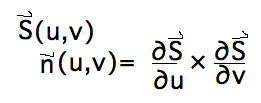- Review session
- Tomorrow (Tuesday, Dec. 15), 1:00 - 2:30
- Welles 123
- SOFIs
- Helpful to me in teaching this (or other) courses in future
- Access through myGeneseo/KnightWeb
- End tomorrow!
- Final
- Dec. 17 (Thursday), 8:00 AM, usual classroom
- Comprehensive but emphasizing material since 2nd hour exam (e.g., multiple integrals, line integrals, vector fields, conservative vector fields, Green’s Theorem, etc.)
- Rules and format similar to hour exams, especially open references
- Except designed for 2 hours, you have 3
- Donuts and cider
- What they mean
- Divergence measures whether flow is diverging/expanding (positive) or converging/contracting (negative)
- Curl is a vector about which field is circulating
- But neither “circulation” nor “divergence/convergence” are exactly what you intuitively think of them as when looking at, e.g., a plot of a vector field
- Example
- Find divergence and curl of F(x,y,z) = ⟨ xy, yz, zx ⟩
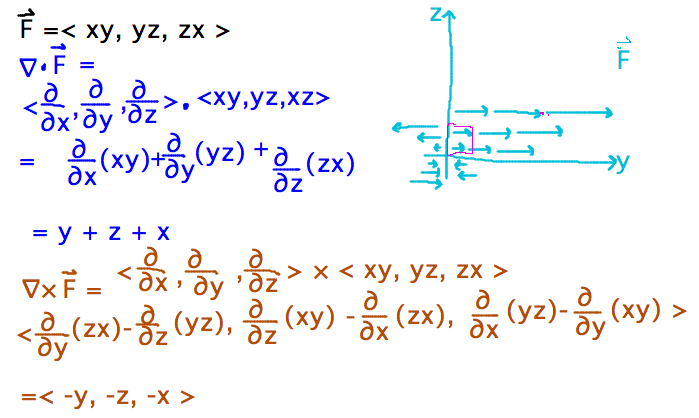
- Find divergence and curl of F(x,y,z) = ⟨ xy, yz, zx ⟩
- Consider what parameterization ⟨ cosu, sinu, v ⟩ looks
like as u and v vary
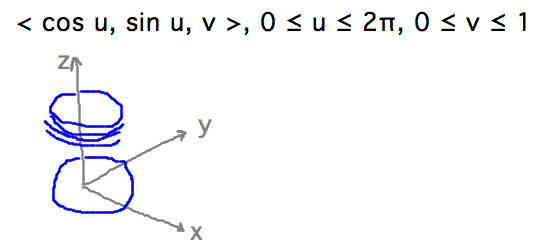
- Parameterizing by independent u and v yields a surface in 3 dimensions
- muPad can do these plots via
plot::Surface - Example — a sphere
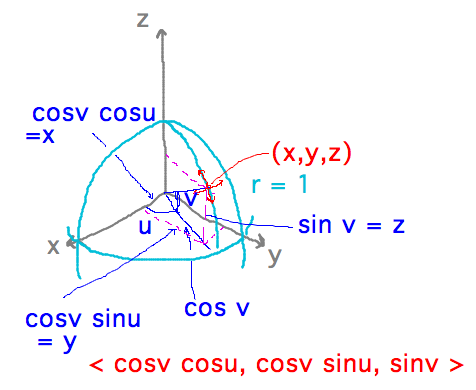
- Can find normals to parametric surfaces, e.g., for computing surface area