- Review session
- Tuesday, Dec. 15, 1:00 - 2:30
- Welles 123
- SOFIs
- Helpful to me in teaching this (or other) courses in future
- Access through myGeneseo/KnightWeb
- Final
- Dec. 17 (Thursday), 8:00 AM, usual classroom
- Comprehensive but emphasizing material since 2nd hour exam (e.g., multiple integrals, line integrals, vector fields, conservative vector fields, Green’s Theorem, etc.)
- Rules and format similar to hour exams, especially open references
- Except designed for 2 hours, you have 3
- Donuts and cider
- Integrate field F(x,y) = ⟨ x+y, y-x ⟩ around curve defined by
y = 2 - 2x2, x = 0, y = 0 by directly integrating line
integral (should get -2 2/3)
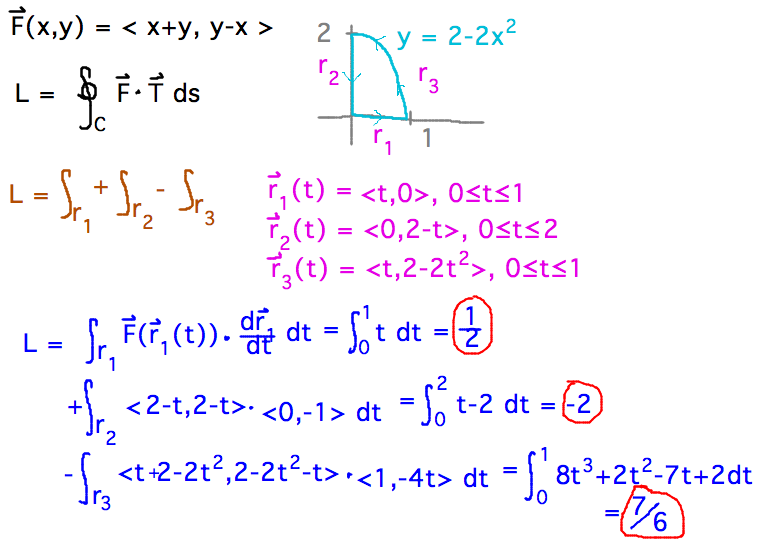
- Find flux of F across the curve

- Integrate F(x,y) = ⟨y, -x ⟩ along half-circle x2
+ y2 = 1 from (1,0) to (-1,0)
- Trick question! Green’s Theorem doesn’t apply to non-closed curve
- How to tell when to use which form of Green’s Theorem?
- Curl form best for integrating components of field parallel to
path, divergence for integrating components perpendicular to path
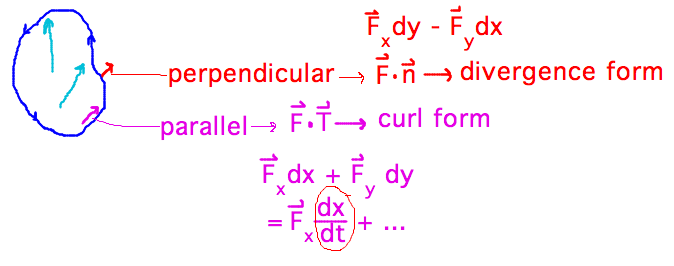
- But this begs the question of how you know what components of the field you’re interested in, and for that you often need additional knowledge of the thing being modeled by the integral
- Curl form best for integrating components of field parallel to
path, divergence for integrating components perpendicular to path
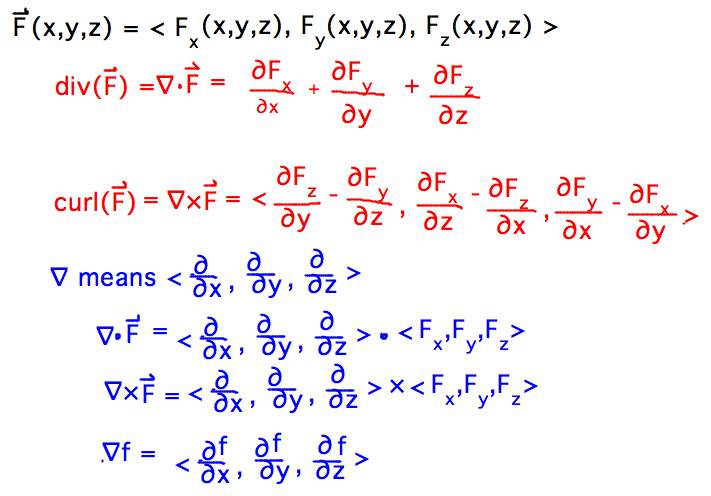
- Curl of any gradient field = ⟨0,0,0⟩
- This is where component test for a conservative field comes from
- A bit more re divergence and curl
- Parametric surfaces
- From section 16.5 (but you don’t need to read it)