- Constraint for cylinder-in-sphere problem?

- Summary of section 15.2
- Different ways to integrate more generally over regions
- Stronger form of Fubini’s theorem
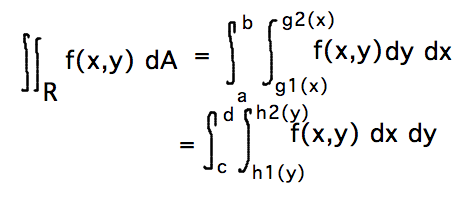
- Different ways to integrate more generally over regions
- Examples
- Volume between z = x2 + y2 + 1 and triangle
0 ≤ x ≤ 1 and y ≤ x
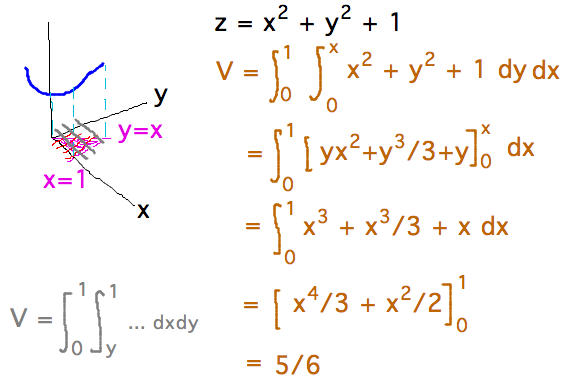
- Volume between z = 2x + y + 2 over 0 ≤ y ≤ 1-x2
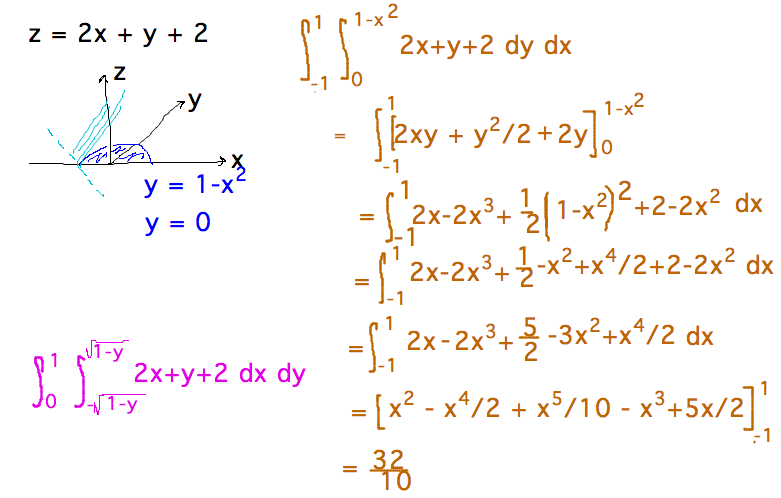
- Small changes in this problem could put z < 0 over some of the region of integration; to compute volume between z and xy plane would then require splitting region to avoid negative “volumes” cancelling positive ones
- Volume between z = x2 + y2 + 1 and triangle
0 ≤ x ≤ 1 and y ≤ x
- Area and average value
- Read section 15.3