- Section 15.1
- Definition of double integral
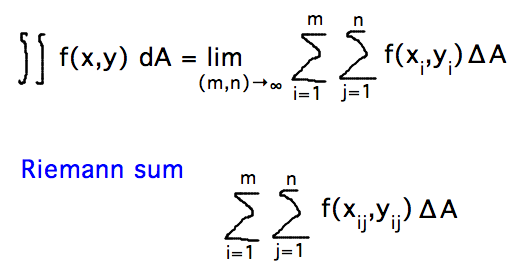
- Key ideas, and a simpler definition
- Divide region into small rectangles
- Norm = size of largest rectangle
- Number of rectangles approaches ∞ as norm approaches 0
- 2-dimensional order of rectangles doesn’t really matter
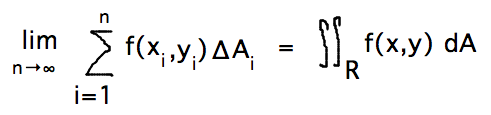
- Double integral can find volume under surface
- Definition of double integral
- Examples
- Integrate x siny over 0 ≤ x ≤ 1, 0 ≤ y ≤ π
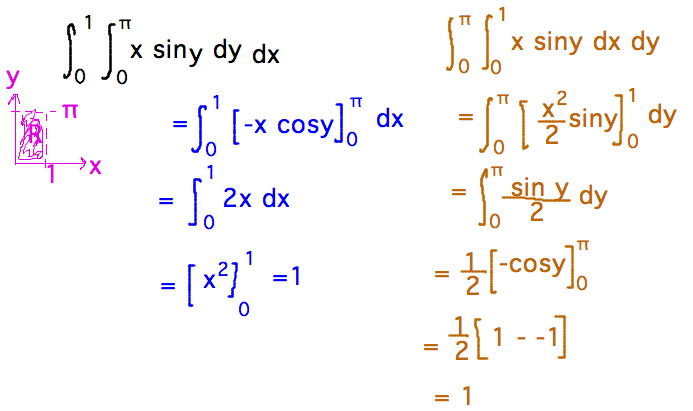
- Volume under z = x2 + y2 + 1 over rectangle -1 ≤ x ≤ 1, -1 ≤ y ≤ 1
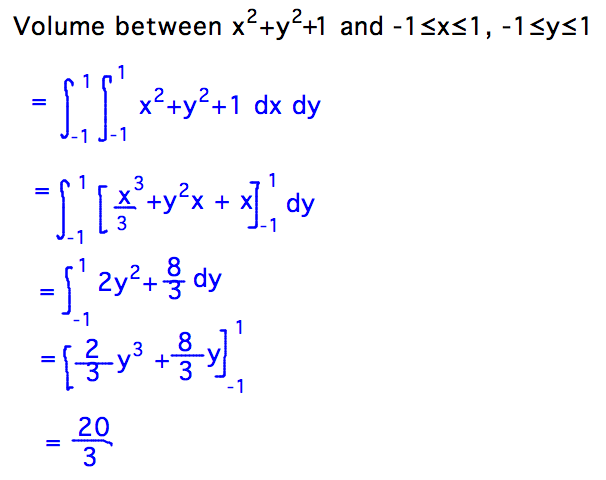
- Look at this problem with muPad, particularly how it can do
symbolic and numeric integration

- Look at this problem with muPad, particularly how it can do
symbolic and numeric integration
- Integrate x siny over 0 ≤ x ≤ 1, 0 ≤ y ≤ π
- How would an indefinite multivariable integral relate to derivatives?
Why don’t people talk about such integrals?
- Integration with respect to x then y inverts differentiation with respect to y then x
- So Fubini’s theorem about order of integration complements/corresponds to mixed derivative theorem about order of differentiation
- But what would be a simple constant of integration in a one-variable integral becomes pretty much any function of all variables except the one you’re integrating with respect to in a multivariable integral, which makes such integrals hard to get much use from
- Problem set
- Integration over non-rectangular regions
- Read section 15.2