- Colloquium
- “The Group Menagerie”
- Dr. Elizabeth Wilcox, SUNY Oswego
- Thursday (tomorrow), Oct 15, 4:00
- Newton 202
- Extra credit for short write-ups, as usual
- Typo in problem set 5 handout
- Question 5, book has lim(x,y)→(1,1), handout has lim(x,y)→(0,0)
- Problem is essentially the same either way you read it though
- Section 14.2
- Properties of limits are similar to properties for single-variable functions
- Continuity of composite functions?

- Definition of limit?
- Similar to other definitions of limit: function can get arbitrarily
close to L by making arguments sufficiently close to (a,b)
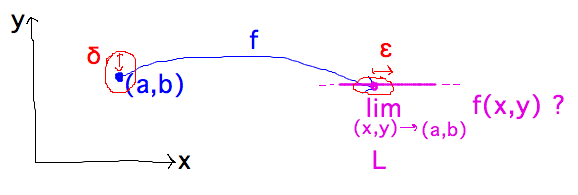
- Similar to other definitions of limit: function can get arbitrarily
close to L by making arguments sufficiently close to (a,b)
- How can boundary point of domain not be in domain?
- Domain: values on which f is defined
- Boundary of any set S: points t such that every circle around t contains some point(s) in S and some point(s) not in S
- This is not like your intuitive sense of a boundary as the
outer-most part of something
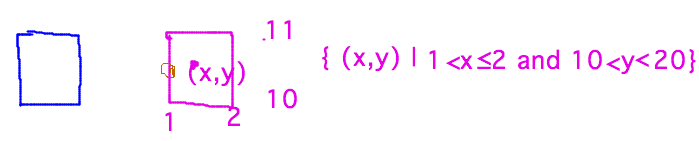
- Cancelling factor in example 2 because point not in domain?
- Handles technical issue that after cancelling common factor from numerator and denominator you have a different function, because it’s continuous at some point(s) where it wasn’t before
- Observing that affected point(s) not in domain means that talking about limit of original function based on new one is still valid
- Partial derivatives
- Read section 14.3