- Colloquium coming up Thursday after break (Oct. 15, 4:00) - more then
- Section 14.1
- Closed, open, boundary, etc. definitions
- Closed = region contains all boundary points
- Open = contains only interior points
- Graphing
- Graphs
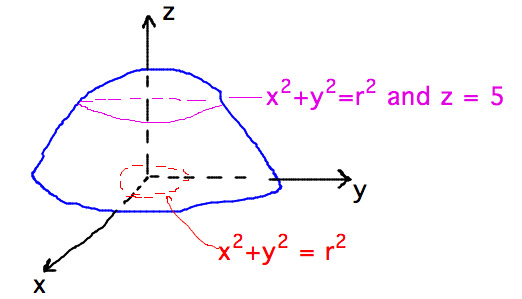
- Level curves
- Level curves vs contours?
- Similar, except contours are lines of constant height around a surface, and so have a specific z coordinate
- Level curves are contours’ projections into the X-Y plane,
i.e., they show the X and Y pairs that produce some constant
height but not explicitly what that height is
- Examples
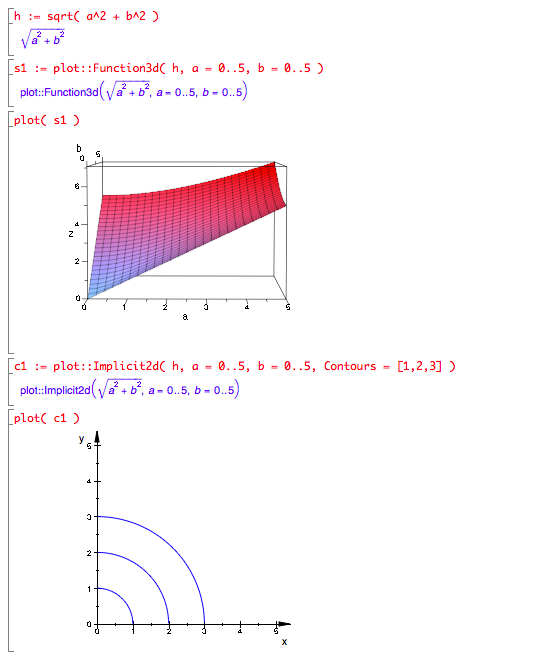
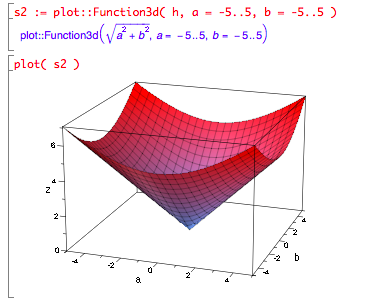
- Hypotenuse of a right triangle as function of a and b?
- h(a,b) = √(a2 + b2)
- (A familiar example of a multi-variable function)
- Distance between 2 points on plane as function of x1,
y1, x2, y2?
- d(x1,x2,y1,y2) = √( (x2-x1)2 + (y2-y1)2 )
- (An example of a function with many variables)
- Graph of hypotenuse function. What about level curves? How do graphs relate?
- What is domain of this function really?
- The whole plane
- (Which makes the domain open because every point in it is
an interior point, but also closed, because all 0 points on the
boundary are in the set—an example of a strange but
valid principle called “vacuous truth”)
- What is domain of this function really?
- Try using muPad to graph f(x,y) = √(4-x2y2)
- Hypotenuse of a right triangle as function of a and b?
- Problem set
- Limits of multi-variable functions
- Read section 14.2