- Chain rule:
- Derivatives of f(g(x)) e.g., √(x2-3)

- Derivatives of f(g(x)) e.g., √(x2-3)
- Section 7.1
- Horizontal line test
- f is 1-to-1 if all horizontal lines across graph hit at most 1 point on graph
- To find inverse
- Book gives 2 steps:
- Rewrite equation for x in terms of y
- Switch x and y
- Or other order
- e.g., f(x) = y = x2 + 1, x ≥ 0
- Step 2: x = y2 + 1, y ≥ 0
- Step 1: x - 1 = y2
- y = √(x-1)
- Notice that restriction x ≥ 0 is needed to make the
function 1-to-1 over the relevant domain, which in turn
allows function to have an inverse function
- Without the restriction, inverse would have to be y = ±√(x-1), which isn’t a function
- Book gives 2 steps:
- Slope of f-1 is reciprocal of slope of f
- f-1′ = 1 / f′( f-1(x) )
- e.g., f(x) = x2 + 1
- f-1(x) = √(x-1)
- f′(x) = 2x
- f-1′(x) = 1 / 2√(x -1)
- Horizontal line test
- Examples and Applications
- Find inverse, and its derivative, of f(x) = x3 - 2
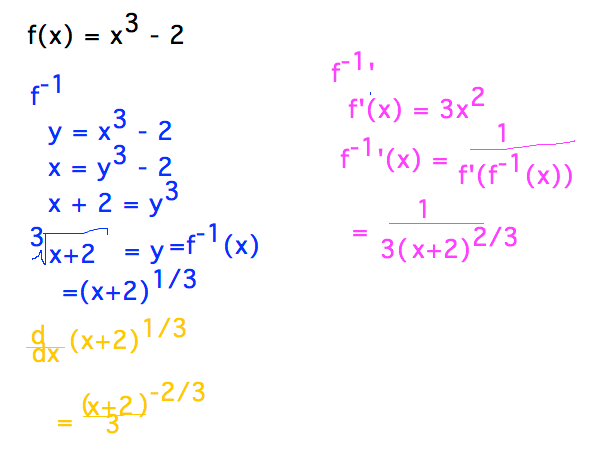
- Find inverse, and its derivative, of f(x) = x3 - 2
- Problem Set
- The natural logarithm
- Read section 7.2