SUNY Geneseo Department of Mathematics

Derivatives and the Shapes of Graphs, Part 2

Wednesday, April 3

Math 221 03
Spring 2019
Prof. Doug Baldwin

Misc

Mid-Semester Feedback

Don’t break up pictures in Canvas? Decision: keep breaking them up, but also provide a link to the original.

Avoid conflicts between SI sessions and extra credit colloquia. This would be nice, but too many people schedule those independently, with too many other constraints (e.g., when rooms are available).

Have more practice problems for exams, label with topic. Decision: I can probably do this. Also remember that there are tons of practice problems in the textbook and online.

Audio record classes as supplement to notes. Nice idea, but would probably be too much work to do now.

Don’t assume students are all experts, explain things in “baby steps” when necessary. A good idea that I’m willing to do, but because there are lots of people with different backgrounds in this class, the ones who want more detail about something can help by asking a question, or just asking for more explanation, etc.

Don’t make problems in problem sets or exams too complicated, avoid confusing wording in questions. This is hard in practice because the fact that problem sets challenge you is an important part of learning, I want a range of problem difficulties in them. It’s a little easier with exams, where challenge-for-learning isn’t the point, but it’s still important that the problems are hard enough to show what you have (and haven’t) learned.

Make problems in one place similar to those in others, e.g., problem set problems similar to class problems, exam problems similar to problem set or class problems. e.g., the table on exam 1. Similar to the point above, problem set problems are supposed to lead you to new or expanded or improved understanding of calculus, so they can’t be just like the ones from class. And exam questions, particularly with open-book tests, need to be at least a little different from things you can look up. But I agree that the table-based question on exam 1 was a little far from anything you had seen before.

Be more sympathetic in grading. There’s a tension here between grading being objective and transparent vs being sympathetic. For the sake of fairness, everyone has to be graded against the same expectations (laid out in the lists of outcomes at the beginning of each problem set).

Spend class time teaching the class. This is a “flipped” class, i.e., one where initial exposure to the ideas comes outside of class meetings, and the face-to-face time is used for active learning and discussion. Both personal experience and education research show that such a style of teaching/learning works better (e.g., better retention of material, better test scores) than traditional lecture. But it can feel like students “learn everything on their own,” because of the need to get that initial understanding outside of class. Please also remember that coming into class to ask questions about the things you want “lecture” explanation of is fine, and that the in-class activities aren’t tests of whether you understand the things you read, they are things that build you understanding of it through working with the ideas, having a chance to talk them over with other students, seeing what the class solution is, etc.

For people who feel they are struggling with the material in this course: please talk to me or Maddie about it, we will try to help.

And for all the issues raised above, there are also people who are overall satisfied with the teaching style and grading.

Exam 2

Covers material since first exam (e.g., implicit differentiation, related rates, initial value problems, linear approximation, extreme values, shapes of graphs — roughly the material on problem sets 5 and 6).

Rules and format otherwise similar to first exam, especially open-references, open-calculator/computer, rules.

SI Session

Questions?

Extreme Values

Last class we looked at the function y = x - x^1/3 . We found dy/dx = 1 - 1 / 3x^2/3, and that it had critical points at ± √1/27 and 0. We also thought the derivative was...

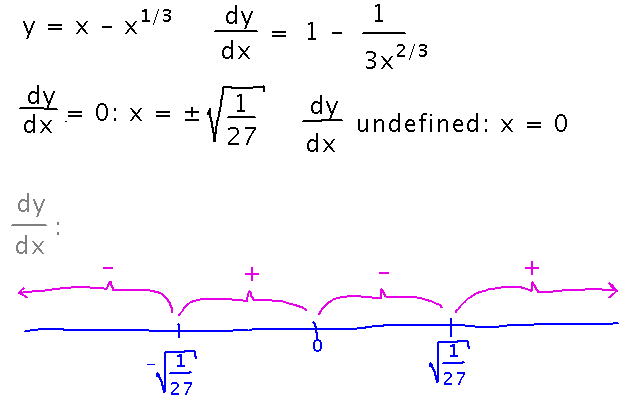
Check these signs, and then figure out what they mean for how the critical points correspond to extreme values. We can check signs with Mathematica, but beware with many powerful calculators, raising negative numbers to fractional powers is problematic: such powers can be complex, and it can be hard to tell when that is the case, so many tools just throw up their hands and refuse to do it (e.g., Excel last time). Try to write such calculations to avoid fractional powers (e.g., use roots and whole-number exponents as separate calculations). Here is an example Mathematica notebook in which we calculated values of dy/dx for this problem (by inserting different values for x into the same expression and re-evaluating, to save re-typing; the notebook just shows the last calculation).

These calculations showed that the original ideas about the sign of dy/dx were wrong in places. Here are the corrected values, and rough sketches of what the derivative and original function might look like:

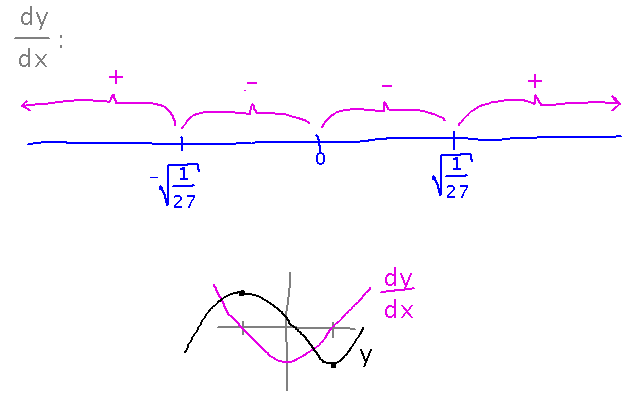
(Click here for the complete picture for the above example as it looked at the end of class.)

Key Points

The sign of the derivative helps you tell where a function is increasing or decreasing, and thus which critical points are maximums, minimums, or neither.