Integration by Substitution, Part 2

Return to Course Outline

Previous Lecture

Miscellaneous Questions?

Derivatives in Mathematica

There are 2 ways you can have Mathematica find a derivative.

The first and slightly more flexible is to define a function whose derivative you want, and then use the ′ (single quotation mark, or prime symbol) operation on it. You can take second (and probably higher) derivatives by writing multiple prime symbols:

This method also gives you a function you can do other things with (e.g., plot, evaluate, etc.), and produces derivatives that can themselves be saved as functions.

The second method is to use the D function introduced several months ago:

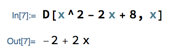
This is maybe a little simpler than functions and prime symbols, since you don’t have to define the function whose derivative you want in advance, but there’s less you can do with it in the long run.

Download this notebook to see and experiment with both ways of taking derivatives in Mathematica.

Right Riemann Sums

A right Riemann sum is just a Riemann sum in which the x value at which to calculate the height of each rectangle is the x value at the right edge of that rectangle (in contrast to a left Riemann sum, in which the chosen x values are at the left edge of each rectangle):

The formula to find a right Riemann sum is basically the same as for any Riemann sum, but I find the “x_i*” value particularly easy to calculate: it’s the starting point for integration plus the rectangle number times the width of the rectangles:

Summary of Substitution Discussion

Particularly those parts not covered in the November 23 class notes. Also see section 5.5 in the textbook.

Multiples of the Derivative

One way to think of substitution is that you’re trying to replace part of a hard-to-evaluate integrand with a dummy variable (u) that makes the integral easier to find. But when making this replacement you need to replace all occurrences of the original variable, even in differentials (e.g., “dx”), with the new variable.

(A little more precise way to think of substitution is that it’s the antiderivative rule that corresponds to the chain rule for derivatives. So you’re trying to view an integrand as an “inner function,” the “g(x)” in the chain rule, to which an “outer function,” the “f’(g(x))” from the chain rule, is applied, all of which is multiplied by the inner function’s derivative, the “g’(x)” from the chain rule.)

Whichever way you prefer to think of substitution, it’s often the case that you don’t find the derivative of u in the integrand, but rather some constant multiple of it. In these cases, the constant often becomes something you can explicitly factor out of the integral after substitution. For example....

As another example, try integrating xe^2x2-1.

Here the best candidate for u is 2x²-1, whose derivative is 4x dx, but the integrand only provides x dx to match this. So replace x dx with 1/4 du:

Next

Substitution in definite integrals.

Please read “Substitution for Definite Integrals” in section 5.5 of the textbook by class time Wednesday.

Please also join in this discussion of definite integrals with substitution by class time Wednesday.

Next Lecture