Limits at Infinity

Return to Course Outline

Previous Lecture

Misc

Hour exam 2 is next Monday (November 4).

Covers material up through problem set 8 that wasn’t covered on the first hour exam, i.e., problem sets 6 through 8. Topics include, for example, the chain rule; implicit differentiation; derivatives of exponential, logarithmic, and inverse functions including inverse trig; related rates; extreme values; Mean Value Theorem.

Rules and format similar to first hour exam, especially open-references-closed-person rule.

Extended SI session Thursday, 5:00 - 8:00, Fraser 104.

Questions?

Limits at Infinity

Section 4.6.

Key Idea(s)

Some new limit laws give intuitively natural results about, e.g., limits of functions of the form xⁿ and 1/xⁿ for positive integers n.

A strategy for finding limits at infinity of rational functions:

1. Divide the numerator and denominator by the highest power of x in the denominator (thereby getting non-negative powers of x in only the numerator or denominator)
2. Apply the quotient limit law
3. You can now evaluate the limit, probably also using limit laws for xⁿ and 1/xⁿ.

This strategy leads to some shortcuts too.

Horizontal asymptotes are finite constant values that functions approach in the limit as x approaches positive or negative infinity.

Rational Function Example

Look at Example 4.25 in the book, and see if you can adapt its methods to finding the limits as x approaches positive and negative infinity of (3x³ + 4x²) / (x² + 2x).

For the limit as x approaches positive infinity, start by factoring x² out of the numerator and denominator and canceling.

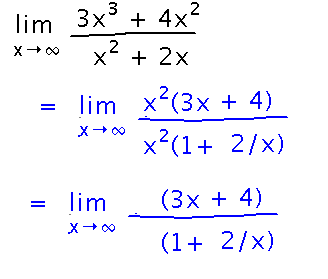
Then apply the quotient limit law, and take limits of the numerator and denominator. Note that this involves using the new limit laws.

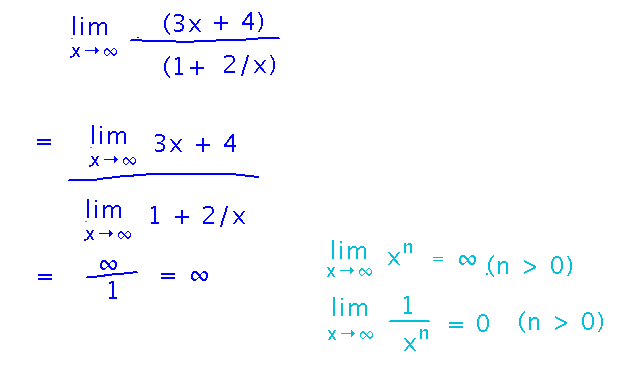
Consciously Using the “Key Idea” Strategy

What is the limit as n approaches infinity of (n² + n)/2n²?

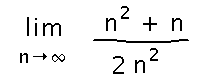
Start by factoring the highest power of n in the denominator out of both numerator and denominator and canceling:

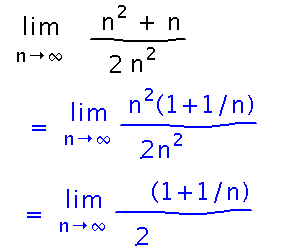
Then use the quotient limit law:

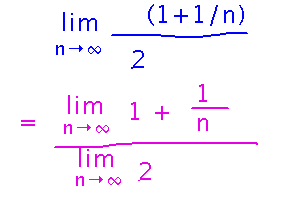
And finally take the limits in the numerator and denominator:

Notice that this is an example with a horizontal asymptote:

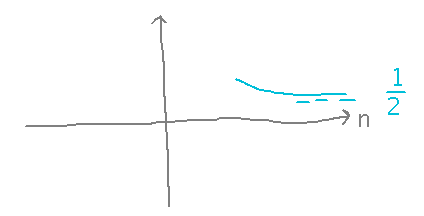
This is also an example that allows one of the shortcuts for limits at infinity, namely if the numerator and denominator have the same highest power of n (or x) then the limit is the ratio of those terms’ coefficients.

Example at Negative Infinity

Returning to the first example, what is its limit as x approaches negative infinity?

The first steps in solving this are the same as when x approaches positive infinity, namely factoring x² out of numerator and denominator and canceling. The main difference is that the limit in the numerator is different, because it has x raised to a positive odd power, which yields a negative result when applied to a negative number.

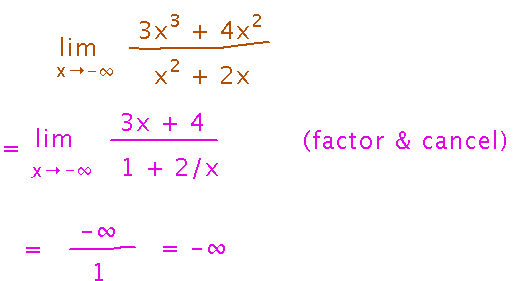
In terms of end behavior, this function’s graph thus rises indefinitely for large positive x, and falls indefinitely for large negative x:

Extension

Consider this limit:

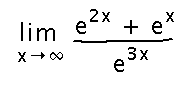
It will probably appear on the next problem set. But you can approach it using similar ideas to what we did today, namely dividing by the highest power in the denominator, and then using limit laws dealing with limits of e^x and e^-x.

Next

Optimization problems.

Read section 4.7.

Next Lecture