SUNY Geneseo Department of Mathematics

The Fundamental Theorem of Calculus, Part 2

Friday, November 10

Math 221 05
Fall 2017
Prof. Doug Baldwin

Questions?

Question 4

How do you set up the “limits of Riemann sums” for question 4 on problem set 9?

Start by figuring out how the parts of the generic limit formula for a definite integral map to the specifics of this problem: what are the x values from which to calculate the heights of rectangles, what are the widths of the rectangles, what is the function f, etc.

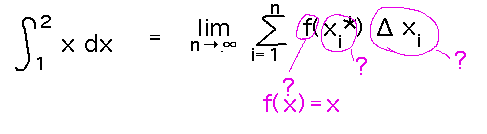
Need to identify x_i*, Delta x_i, f in limi as n approaches infinity of the sum of f(x_i*) Delta x_i

Then rewrite the sum in those terms, find a closed form for it, and take the limit of the closed form.

The Fundamental Theorem, Part 2

Introduction

Find the integral of √x - cos(x) from x = 0 to x = π/2.

Reading ideas: To integrate f(x) from a to b, compute F(b) - F(a) where F is an antiderivative of f.

Solution:

F(x) = 2/3 x^(3/2) - sinx so integral = 2/3 (pi/2)^(3/2) - 1

Significance

Where does part 2 come from, i.e., what previous calculus ideas justify it?

Mainly the mean value theorem, providing just enough connection between derivatives and antiderivatives to connect a Riemann sum to a difference of antiderivatives.

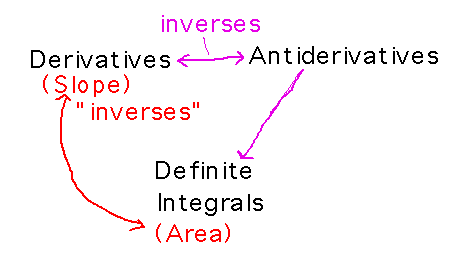
What does the fundamental theorem (both parts) mean?

It establishes connections between the various areas of calculus.

And therefore a somewhat surprising connection between slopes and areas as being in some sense inverse issues

Derivatives (slopes) are inverses of antiderivatives, which underlie definite integrals (areas)

Definite Integrals

Integrate 2x² + 3x - 5 from x = 3 to x = 5

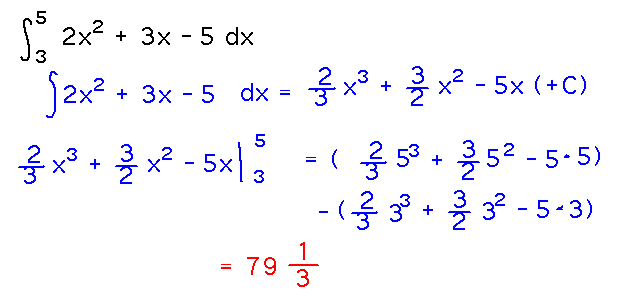
Integral from 3 to 5 of 2x^2+3x-5 = 2/3 x^3 +3/2 x^2 - 5x evaluated from 3 to 5 = 79 1/3

More applications of definite integrals.

Read section 5.4

Next Lecture