More about the Fundamental Theorem of Calculus

Return to Course Outline

Previous Lecture

Questions?

Proof

How the proof of part 1 of the Fundamental Theorem draws on previous properties of definite integrals.

Average Value

How to define the average value of a function is tricky — you can’t add up the value at every point and divide by the number of points because there are an infinite number of points.

Instead, the average value of a function is defined as an integral, with results that correspond well to intuition:

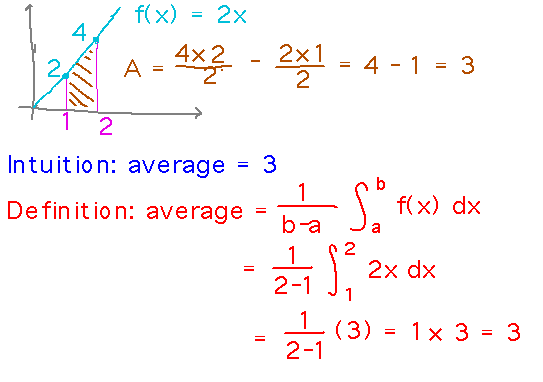
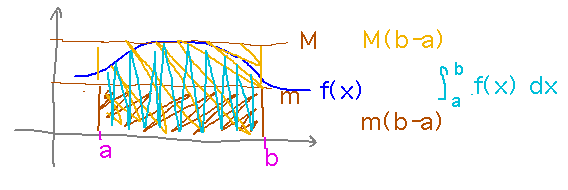
Comparison Theorem

A theorem that gives bounds on the values integrals can have. In this case the bound is determined by bounds on the value of the function:

Split Intervals

An integral over a long interval can be split into the sum of several integrals over adjacent shorter intervals:

Next

Part 2 (“Fundamental Theorem of Calculus, Part 2: The Evaluation Theorem”)

Next Lecture