Extreme Values

Misc

Exam 2

It’s currently scheduled for next Friday, October 27.

Moving it to the following Thursday (November 2) would mean having it in our Fraser room where you have more space, and possibly providing more time to cover material that logically belongs on it.

But it might also mean starting material before the exam that won’t be on it, and possibly disrupting plans made around the original date.

Any thoughts from you on which you prefer?

Problem Set

Hand out problem set on related rates and linearization.

Questions?

Maxima and Minima

Section 4.3

Example. Use the derivative to find a local maximum of y = 4 - x².

Reading ideas: The sign of the derivative corresponds to the function increasing (+) or decreasing (-), so look for places where the derivative crosses the x axis, i.e., where it equals 0.

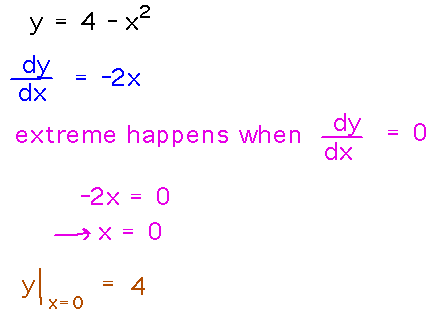
Example. Find a local minimum of y = |x|.

Reading ideas: In addition to places where the derivative is 0, also look for places where the derivative is undefined.

Theory

Flesh out the proof of Fermat’s theorem to show that f′(c) ≥ 0.

The part of the proof shown in the book establishes that if x = c is the location of a local maximum of f, and f is differentiable at c, then f′(c) ≤ 0. It tells the reader that they can “similarly” show that f′(c) ≥ 0, and can “similarly” argue in the case that f(c) is a local minimum.

The argument that f′(c) ≤ 0 uses the definition of the derivative as the limit of (f(x)-f(c))/(x-c), and then breaks that limit into 2 one-sided limits. Since f(c) is a local maximum, f(x) - f(c) is always 0 or less. In the limit from the right, where x > c, x - c will be 0 or greater, essentially turning the quotient into a negative number over a positive one, which is negative (or 0). Thus f′(c) ≤ 0.

The “similar” argument that f′(c) ≥ 0 uses the limit from the left, where x < c. Now the quotient is essentially a negative number over another negative one, which is positive (or 0). Thus f′(c) ≥ 0.

Since f′(c) exists (because f is differentiable), the only way that f′(c) can be simultaneously less than or equal to 0 and greater than or equal to 0 is if it is equal to 0.

Another Example

Example. Find the absolute extrema of y = 2x³ + 3x² - 12x + 1 over [-4,2].

Reading ideas: There is a 3-step process for finding absolute extrema:

1. Evaluate f at the endpoints of the interval in question.
2. Find critical points (via the derivative) within the interval and evaluate f at each.
3. Compare the values found in steps 1 and 2; the largest is the absolute maximum and the smallest is the absolute minimum in that interval.

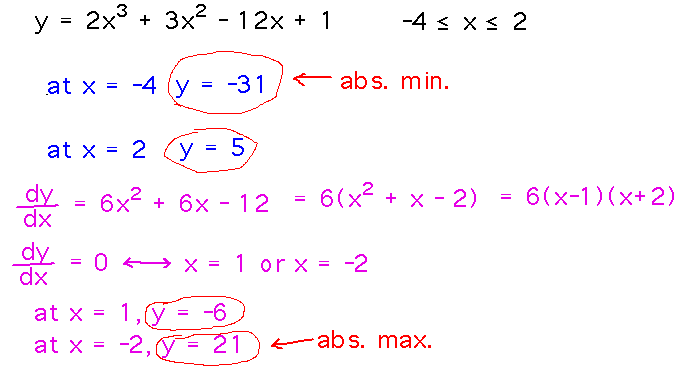
Computer algebra systems or similar technology tools start to show their value here, since they can do much of the differentiating, solving for 0, evaluating functions, etc. that problems like this call for:

Take Aways

Local extrema can only happen where a function’s derivative = 0 or is undefined - the so-called critical points.

Absolute extrema can happen at critical points or at the endpoints of the interval in question.

Keep computer algebra systems in mind as tools for solving problems.

Next

Start the Mean Value Theorem.

Read section 4.4.