Linearization

Misc

Class by Video?

It was awkward at times, either socially or technically.

Socially because you could withdraw more from class (but for some that made it more comfortable than being put on the spot to say things) and I didn’t always know how the class was reacting to ideas.

Technically the audio feedback was annoying. But listening through headphones helped that. Also, conversations, or parts of them, meant for others in the same room were sometimes picked up by microphones and taken as comments for the whole group.

If you have other comments you’d like to share, feel free to email me or bring it up at the end of a meeting, etc.

Questions?

Linearization and Differentials

Section 4.2

Examples

Example. Find a linear approximation to f(x) = x + sin x near x = 0.

Reading question: what is a “linear approximation” to a function?

• The realization that over a short enough interval, any function is approximately a straight line.

Other reading ideas

• The formula for the linearization of f around a is L_a(x) = f(a) + f′(a)(x-a)
• This is just an adaptation of the point-slope formula for a line through point (a,f(a)) and with slope f′(a): y = y₀ + m(x-x₀)

You can also use this formula to find a linearization about x = π/2.

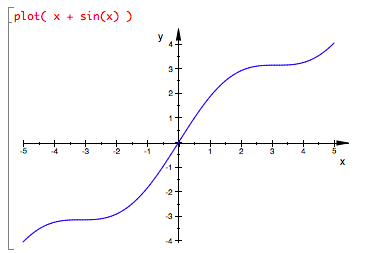
L₀(x) = 2x from above says that the linear approximation to y = x + sinx near x = 0 rises 2 units for each 1 unit change in x, and intersects the y axis at y = 0 (i.e., y = 2x + 0 read as y = mx + b gives m = 2 and b = 0). This is very close to the actual behavior of the graph of y = x + sinx:

Example. If y = x³, estimate how much y changes by when x changes from 10 to 10.1.

Reading ideas

• Use the formula dy = f′(x) dx
• This formula acknowledges that dy and dx are “differentials,” i.e., small changes in y or x that can often be treated as forming a fraction which can be manipulated as other fractions are, even though dy or dx by themselves are never exactly equal to any number. (As used in the above formula, dy is an approximation to the actual change in y, and “dx” is a bit of a misnomer for a small but measurable change in x.)

Take-Aways

All curves are approximately linear over small enough intervals.

You can therefore use the slope (i.e., derivative) of a curve to estimate values near the place the slope was calculated.

Differentials are a thing, and useful for relating changes in one variable to changes in another, even if they aren’t exactly numbers.

Next

Derivatives, maxima, and minima.

Read section 4.3