- Email me colloquium reactions
- SOFIs
- Final Exam
- Tuesday, Dec. 16, 8:00 AM
- Usual classroom
- Comprehensive but emphasizing material since 2nd hour exam (e.g., Riemann sums, fundamental theorem, definite integrals, substitution, volumes, etc.)
- Designed for 2 hours, you’ll have 3
- Otherwise similar rules and format to hour exams, esp. open references and computers
- Donuts and cider
- Review session
- Study day (Tuesday, Dec. 9), 3:30 - 5:00 PM
- Sturges 208A
- Bring your questions/topics
- Optimization question from hour exam?
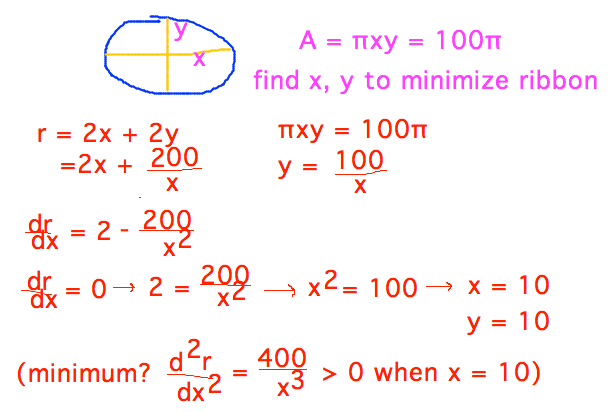
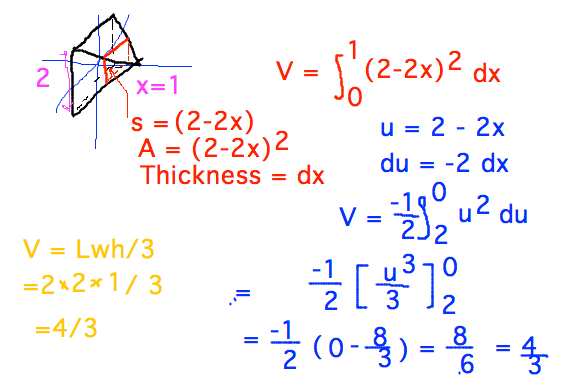
- Pyramid example
- Section 6.1
- Volumes via cross sections
- Volume extending from a to b and with cross-section area A is integral from a to b of A dA
- Steps
- Sketch solid and cross-section
- Find formula for A(x)
- Find limits of integration
- Integrate A(x)
- Volumes based on disks for rotation about x and y, volumes based on washers for rotation about x
- Examples
- Spin y = sinx around x axis

- Illustrates finding radius of disk as well as integration via combination of trigonometric identity and substitution
- Spin y = x2 around y axis

- Spin y = sinx around x axis
- Modelling alteration of light as it passes though the
world, e.g., in hyper-realistic computer graphics, amounts to
integrating all of the scattering, reflection, etc. it experiences
along its path to a viewer
