- Colloquium
- Wednesday, Dec. 3, 2:30 PM
- Newton 201
- “Learning with Leibniz”
- Prof. Olympia Nicodemi
- Extra credit for going and writing a 1-paragraph summary/review
- SOFIs
- Final Exam
- Tuesday, Dec. 16, 8:00 AM
- Usual classroom
- Comprehensive but emphasizing material since 2nd hour exam (e.g., Riemann sums, fundamental theorem, definite integrals, substitution, integral applications, etc.)
- Designed for 2 hours, you’ll have 3
- Otherwise similar rules and format to hour exams, esp. open references and computers
- Donuts and cider
- Review session
- Study day (Tuesday, Dec. 9), 3:30 - 5:00 PM
- Sturges 208A
- Section 5.5
- Using substitution method
- Chain rule in reverse
- If g(x) is differentiable and f(x) continuous, then integral of f(g(x))g′(x)dx is integral of f(u) du where u = g(x)
- Good when function and its derivative are in integrand
- Examples
- Multiple choices of substitutions possible
- Examples
- Introducing a constant coefficient to make substitution
possible and compensating by later multiplying by its reciprocal

- Applying substitutions to polynomials

- A more complicated example

- Introducing a constant coefficient to make substitution
possible and compensating by later multiplying by its reciprocal
- Substitution and definite integrals
- Can either do substitution and then replace u with function of
x, as with indefinite integrals, or transform bounds of integration
to u

- Can either do substitution and then replace u with function of
x, as with indefinite integrals, or transform bounds of integration
to u
- Divide volume into thin slices, then add up volumes of all
slices as Riemann sum aka definite integral
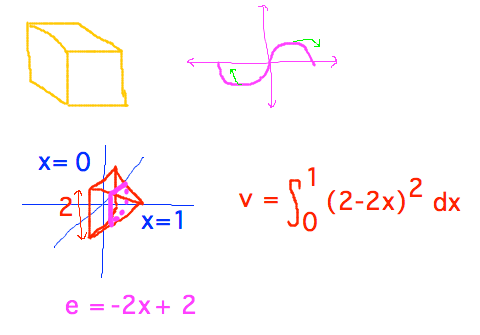
- More volumes via integration
- Do the following:
- Evaluate the integral for the pyramid (integral from 0 to 1 of (2-2x)2)
- Optionally, look up an actual formula for the volume of a pyramid and see if it gives the same value the integral did
- Read section 6.1