- Integral notation for antiderivatives?
- Integral symbol and “dx” (or other variable to integrate with respect to) bracket expression whose antiderivative you’re computing
- Actual antiderivative follows an “=” symbol, and
includes “+ C” constant because integral technically
represents the general antiderivative rather than any specific one

- Economics example
- Suppose the quantity of some product that people are willing to
buy is inversely related to its price:
- q = 1/p
- What is dq/dp, and what does it reflect?
- Sensitivity of sales to price
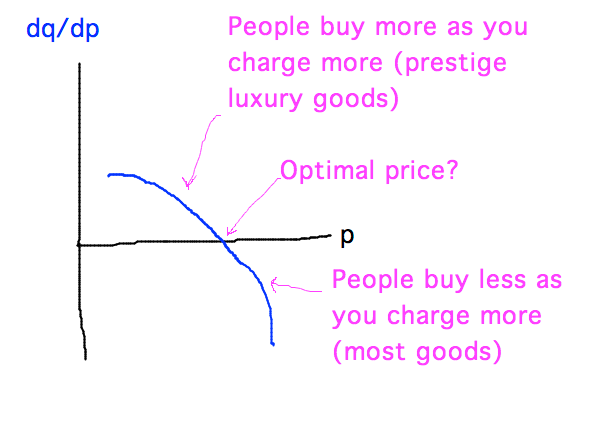
- (For q = 1/p, dq/dp = -1/p2, which is always negative and isn’t the function graphed above)
- Sensitivity of sales to price
- If the product is some new invention, its price is likely to drop sharply over time, maybe
- p = 1 - (t-1)1/3
- And we still have q = 1/p
- What is dq/dt, and what does it have to do with composition of functions and the chain rule?

- q = 1/( 1 - (t-1)1/3 )
- = ( 1 - (t-1)1/3 )-1
- dq/dt = -( 1 - (t-1)1/3 )-2 ( -1/3 (t-1)-2/3)
- Suppose the quantity of some product that people are willing to
buy is inversely related to its price:
- Section 3.7
- Does implicit differentiation give same results as explicit differentiation?
- Use implicit differentiation to find dy/dx given that 3x - 2y = 1
- What shape is this curve, what is y as explicit function of x? What is explicit derivative dy/dx?
- Rewrite for y as function x
- 3x - 1 = 2y
- y = 3/2 x - 1/2
- dy/dx = 3/2
- Rewrite for y as function x
- Implicit differentiation
- d/dx(3x - 2y) = d/dx(1)
- d/dx(3x - 2y) = 0
- 3 - 2 dy/dx = 0
- -2 dy/dx = -3
- dy/dx = 3/2
- Can you also find dx/dy?
- d/dy(3x - 2y) = d/dy(1)
- d/dy(3x - 2y) = 0
- 3 dx/dy - 2 = 0
- dx/dy = 2/3
- (Not surprising that rate at which x changes in response to changes in y is reciprocal of rate at which y changes in response to changes in x)
- What shape is this curve, what is y as explicit function of x? What is explicit derivative dy/dx?
- Use implicit differentiation to find dy/dx given that 3x - 2y = 1
- Equations of the form ax2 + by2 + cxy + dx + ey + f = 0
- General form for all conic sections including rotations and degenerate cases
- 2D version of 3D “quadric surfaces” in computer graphics, which can describe spheres, cylinders, 3D generalizations of other conic sections, etc.
- For example 3x2 - y2 - 9 = 0
- dy/dx = ?
- 6x - 2y dy/dx - 0 = 0
- -2y dy/dx = -6x
- dy/dx = 3x/y
- d2y/dx2 = ?
- d2y/dx2 = d/dx( 3x/y )
- = ( d/dx(3x) y - 3xd/dx(y) ) / y2 (quotient rule)
- = ( 3y - 3x dy/dx ) / y2
- = ( 3y - 3x 3x/y ) / y2
- = ( 3y - 9x2/y ) / y2
- = ( 3y2/y - 9x2/y ) / y2
- = ( 3y2 - 9x2 ) / y3
- = 3( y2 - 3x2 ) / y3
- Problem set
- Related rates problems
- Section 3.8