The Chain Rule

Return to List of Lectures

Previous Lecture

• Misc
  • Hour exam
    • Tuesday, Oct. 7
    • Material since start of semester (e.g., limits, limit definition of derivative, differentiation rules including product, quotient, trig derivatives)
    • 4 - 6 short-answer questions, e.g., like problem sets
    • Whole class period
    • Open book, notes, computer; closed person
  • Useful fact for trig derivatives problem set
    • Antiderivatives of 1/x are of the form ln x + C
• Questions?
  • Problem set 3 question re derivative of u(x)/v(x) at x = 1
    • Quotient rule: ( u′(x)v(x) - u(x)v′(x) ) / v(x)²
• The Chain Rule
  • Section 3.6
    • Derivative of composite function
    • d( f(g(x)) ) / dx = f′( g(x) ) g′(x)
    • Or if y = f(u) and u = g(x) then dy/dx = dy/du du/dx
    • Proof via limit definition
    • “Outside inside” idea
    • Repeated use of chain rule
    • Power chain rule: d( uⁿ(x) ) / dx = n u^n-1(x) du/dx
  • Chain rule as steps:
    1. Differentiate outer function w/ inner as unit
    2. Multiply by derivative of inner
  • Examples: find f′(x) if…
    • f(x) = √(1-x²)
      • = (1-x²)^1/2
      • Outside function = square root
      • Inside function = 1 - x²
      • f′(x) = 1/2 ( 1-x²)^-1/2 (-2x)
      • = - x / √( 1-x²)
    • f(x) = sin( x² + 3x - 7 )
      • Outer = sin(...)
      • Inner = x² + 3x - 7
      • f′(x) = cos( x² + 3x - 7 ) (2x + 3)
    • f(x) = cos( 5x )
      • Outer = cos(...)
      • Inner = 5x
      • Or
        • Outer = f = cos(u)
        • u = 5x
      • f′(x) = -5 sin( 5x )
    • f(x) = cos⁵x = (cos x)⁵
      • Outer = u⁵
      • Inner = cos x
      • f′(x) = -5 cos⁴x sinx
    • f(x) = cos( x⁵ )
      • Outer = cos
      • Inner = x⁵
      • f′(x) = -sin( x⁵ ) 5x⁴
      • = -5x⁴ sin( x⁵ )
    • f(x) = 1 / ( x³ + 3√x )
      • Do this with and without the quotient rule
      • Quotient rule:
        • u(x) = 1, u′(x) = 0
        • v(x) = x³ + 3√x, v′(x) = 3x² + 3/(2√x)
        • f′(x) = ( u′(x) v(x) - v′(x) u(x) ) / v²(x)
        • = - ( 3x² + 3/(2√x) ) / (x³ + 3√x)²)
      • Chain rule:
        • f(x) = ( x³ + 3√x )^-1
        • Outer = u^-1 = 1/u
        • Inner = x³ + 3√x
        • f′(x) = -( x³ + 3√x )^-2 (3x² + 3/(2√x))
        • = -(3x² + 3/(2√x)) / ( x³ + 3√x )²
    • f(x) = √( sin(x²+1) + cos(x²-1) )
      • Outer = √u
      • u = sin(x²+1) + cos(x²-1)
      • f′(x) = 1/(2√u) u′(x)
      • u′(x) = d(sin(x²+1)) / dx + d(cos(x²-1))/dx
      • d(sin(x²+1)) / dx:
        • Outer = sin
        • Inner = x² + 1
        • d(sin(x²+1)) / dx = 2x cos(x²+1)
      • d(cos(x²-1))/dx:
        • Outer = cos (derivative = -sin)
        • Inner = x²-1
        • d(cos(x²-1))/dx = -2x sin(x²-1)
      • So f′(x) = 1/(2√u) ( 2x cos(x²+1) - 2x sin(x²-1) )
      • = 1/(2√(sin(x²+1) + cos(x²-1)) ) ( 2x cos(x²+1) - 2x sin(x²-1) )
      • = 1/(√(sin(x²+1) + cos(x²-1)) ) ( x cos(x²+1) - x sin(x²-1) )
      • = ( x cos(x²+1) - x sin(x²-1) ) / √(sin(x²+1) + cos(x²-1))
      • = x ( cos(x²+1) - sin(x²-1) ) / √(sin(x²+1) + cos(x²-1))
• Implicit Differentiation
  • (An application of the chain rule)
  • Consider the circle defined by x² + y² = 1
  • Does it have a derivative? If so, what is it?
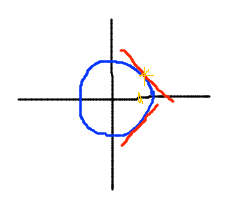
    • Yes, it has a derivative, i.e., a rate at which the Y coordinate of points along the curve is changing relative to changes in the X coordinate, aka a tangent to the curve (at least at most points)
      
  • Option 1 for calculating the derivative
    • y² = 1 - x²
    • y = √(1-x²)
    • But now you have to be careful, either the square root is a function that only yields positive values, or it’s not really being used as a function and you have to remember that its values are both positive and negative
  • Option 2
    • Based on power rule, 2x + 2y (which isn’t quite right, but…)
    • d( x² + y² ) / dx = d(1)/dx  (if 2 things are equal, their derivatives should also be equal)
    • 2x + 2y dy/dx = 0  (use chain rule to differentiate y² with respect to x)
    • 2y dy/dx = -2x
    • dy/dx = -2x / 2y = -x/y
• Next
  • More implicit differentiation
  • Section 3.7

Next Lecture