- Hour exam 2
- Friday, Nov 14
- Material on derivatives since first exam (e.g., chain rule, implicit differentiation, related rates, extreme values, Mean Value Theorem, optimization, etc.)
- Rules and format similar to first hour exam
- Including open book, notes, references
- But probably slightly more questions (7 - 9), and slightly harder questions e.g., more word problems
- Section 4.5
- Optimization often about finding minimum or maximum values
- How to solve optimization problems
- Read problem
- Draw picture
- Introduce variables
- Write equation
- Test critical points & endpoints in derivative
- Examples, e.g.,
- Fermat’s principle: light travels on minimum-time paths
- Snell’s law follows from this: sinΘ1 / c1 = sinΘ2 / c2
- Examples
- Radios, televisions, etc. are tuned to a particular station by an
electrical circuit whose resistance (R) depends on the
frequency (f) of the radio wave according to the formula
- R = (Lf) / (1 + LCf2)
- Where L and C are parameters of the tuner (and hide some constants of proportionality in some versions of the formula). What is the frequency at which resistance is highest for fixed L and C (that’s the frequency the radio/televions/etc is receiving)?
- How to start? find dR/df
- Set dR/df = 0, solve for f
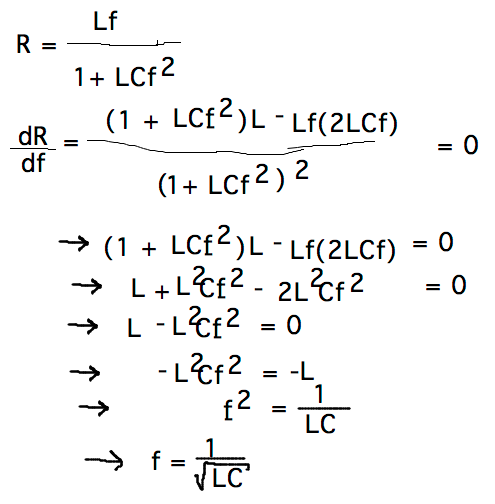
- Do manufacturers of buckets actually use dimensions that
come close to minimizing the amount of material needed to
make the bucket?
- Bucket = cylinder w/ one end closed
- Cost modelled by area
- Even though volume of plastic = surface area times thickness

- Even though volume of plastic = surface area times thickness
- Radios, televisions, etc. are tuned to a particular station by an
electrical circuit whose resistance (R) depends on the
frequency (f) of the radio wave according to the formula
- Finish analyzing buckets
- Introduction to integrals