- Date for hour exam 2
- Choices: Nov 7 (Friday), Nov 10 (Monday), Nov 14 (Friday)
- Exam will cover material on derivatives since first exam (e.g., chain rule, implicit differentiation, related rates, extreme values, Mean Value Theorem, optimization, etc.)
- Probably harder, more word problems, than 1st test
- Section 4.4
- 2nd derivative test for concavity
- If f′′(x) > 0 then graph of f over I is concave up
- If f′′(x) < 0 then graph of f over I is concave down

- Points of inflection: where graph has tangent and concavity changes
- 2nd derivative test for extrema
- If f′(c) = 0 and f′′(c) < 0 then local maximum at c
- If f′(c) = 0 and f′′(c) > 0 then local minimum at c
- If f′(c) = 0 and f′′(c) = 0 then who knows
- Concavity f/ 2nd derivative is helpful in sketching graphs
- 2nd derivative test for concavity
- Examples: Use information about derivatives, asymptotes, etc. to
estimate what the graphs for the following functions look like
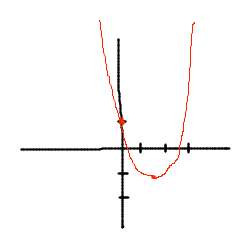
- Warm-up: f(x) = x2 - 3x + 1
- Guess: parabola opening up
- f′(x) = 2x - 3
- f′′(x) = 2
- f′′(x) > 0: concave up
- f′(x) = 0
- 2x - 3 = 0
- x = 3/2
- f(3/2) = -5/4
- f(x) = x3 - 4x2 - 3x + 1
- f′(x) = 3x2 - 8x - 3
- = (3x + 1)(x - 3)
- So f′() = 0 at x = -1/3, 3
- f′(x) < 0 for -1/3 < x < 3
- f′(x) > 0 for x < -1/3 or x > 3
- f′′(x) = 6x - 8
- f′′(x) = 0 at x = 4/3
- < 0 for x < 4/3
- > 0 for x > 4/3

- f′(x) = 3x2 - 8x - 3
- Warm-up: f(x) = x2 - 3x + 1
- Algorithm
- Take first and second derivatives
- Find critical points from 1st derivative
- Find intervals where derivative < 0 or > 0
- Find concave up or down intervals and inflection points from 2nd derivative
- Calculate key points on graph (minima, maxima, x- or y-intercepts, etc.)
- Look for vertical or horizontal asymptotes
- Problem set
- Last one covered by hour exam 2
- Optimization
- Read section 4.5