- How to start problem set question re t - 1/t?
- limh→0( [ ((t+h) - 1/(t+h)) - (t - 1/t) ] / h )
- = limh→0( [ ((t+h)2/(t+h) - 1/(t+h)) - (t2/t - 1/t) ] / h ) {give terms common denominators}
- = limh→0( [ ((t2+2th+h2)/(t+h) - 1/(t+h)) - (t2/t - 1/t) ] / h )
- = limh→0( [ ((t2+2th+h2 - 1)/(t+h)) - ((t2 - 1)/t ] / h )
- = limh→0( [ ((t2+2th+h2 - 1)t/t(t+h)) - ((t2 - 1)(t+h)/t(t+h) ] / h ) {cross-nultiply to create common denominators}
- = limh→0( [(t2+2th+h2 - 1) - (t2 - 1)(t+h)]/ht(t+h) ) {combine denominators}
- From here, you simplify and should find that terms in numerator without an h factor cancel out, leaving you able to cancel the h in the denominator with a common factor of h in the numerator, leaving you an expression into which you can substitute h = 0 without dividing by 0.
- Einstein says the kinetic energy of an object moving very fast is E = mc2 ( 1/√(1-v2/c2) - 1 ) where m is the object’s (rest) mass, v is its speed, and c is the speed of light.
- This is how much energy has to be put into the object to accelerate it from standing still to speed v
- What is the limit of this as v approaches c?
- Probably infinite, since the √(1-v2/c2)
divisor gets closer and closer to 0 as v gets closer to c
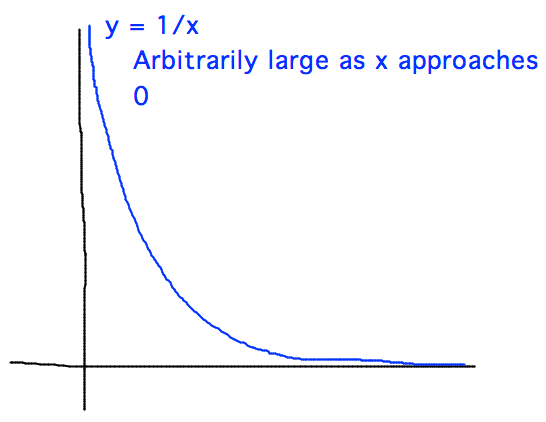
- Can we confirm this?

- New trick: substitute x for √(1 - v2/c2)
and carefully rewrite all uses of v in terms of the new x (in
particular, as v approaches c, the new x approaches 0)

- Note that actually x is approaching 0 from above here
- New trick: substitute x for √(1 - v2/c2)
and carefully rewrite all uses of v in terms of the new x (in
particular, as v approaches c, the new x approaches 0)
- So an object moving at the speed of light has infinite energy.
- Which is impossible, since there isn’t that much energy in the universe
- So no object can move at the speed of light (as long as the object has mass)
- Secondary question: in the “Star Trek” movies and
TV shows, can the star ship accelerate smoothly from a speed below
that of light to one above?
- No, because if it did it would have to travel at the speed of light at some point in time…
- (That’s the Intermediate Value Theorem in action)
- …And we just showed that’s impossible.
- (You just did a proof by contradiction, i.e., assume that something you want to prove—that the star ship’s acceleration and thus speed are discontinuous—is false, and show that the assumption leads to an impossibility)
- Probably infinite, since the √(1-v2/c2)
divisor gets closer and closer to 0 as v gets closer to c
- Section 3.2
- What’s the point?
- This brings us back to the question of rates of change that we started with
- Average rate of change of a function, aka slope of secant line between 2 points on it
- Looked at moving the points really close together to get instantaneous rate of change aka slope of tangent line
- Introduced limits as a way to talk rigorously about “really close together”
- Now we make the connection: instantaneous rate of change aka slope
of tangent is the derivative, defined as limh→0( (f(x+h) - f(x)) / h )
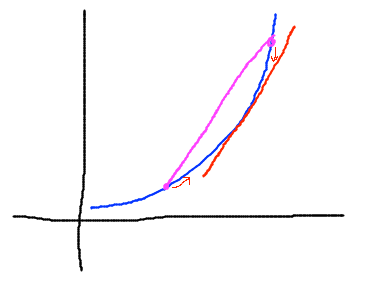
- Examples of derivatives as limits