- “Treasure hunt” in sections 2.4 - 2.6
- What, precisely, does it take to make a function continuous at x = c?
- limx→cf(x) = f(c)
- f(x) defined on both sides of c
- Continuous on an interval [a,b]?
- Right limit as x approaches a = f(a)
- Left limit as x approaches b = f(b)
- f is continuous everywhere in between a and b
- Horizontal line test: If f is continuous, a horizontal line
at any y value between minimum and maximum value of f will
cross f’s graph at least once
![Functions continuous on [a,b] and not because of hole at a](continuous.png)
- What does the Intermediate Value Theorem say?
- Continuous function f on [a,b] and y is value between f(a)
and f(b) then for some a ≤ c ≤ b, f(c) = y
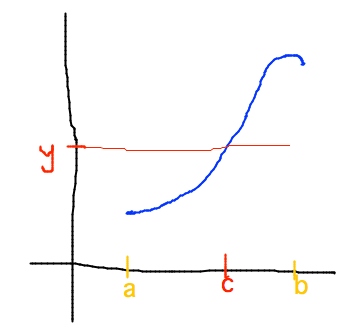
- Continuous function f on [a,b] and y is value between f(a)
and f(b) then for some a ≤ c ≤ b, f(c) = y
- What does it mean to talk about limx→±∞f(x)?
- “End” behavior of f(x)
- Behavior as x gets arbitrarily far from 0
- What does it mean to say that limx→cf(x) = ±∞?
- Vertical asymptote at c
- What is a 1-sided limit?
- Right limit is limit as x approaches a from above
- Left limit is limit as x approaches a from below
- What is an asymptote?
- Line that f(x) approaches but never meets as x approaches ±∞
- Vertical asymptotes exist too

- What, precisely, does it take to make a function continuous at x = c?
- Examples
- Suppose I leave Geneseo at 8:00 some morning, driving to New
York City. At the same time Prof. X leaves Toronto driving to
Geneseo. Is there ever a time when I and Prof. X are exactly
the same distance from Geneseo (although in different places)?
- Yes, difference between distances continuous, positive at
starting time, and negative at end, so it must be 0 at some time

- Yes, difference between distances continuous, positive at
starting time, and negative at end, so it must be 0 at some time
- Find limx→∞( (x+1)/x ).
- Graph looks like asymptote at y = 1, so limx→∞( (x+1)/x ) = 1
- Algebraically...
- limx→∞( (x+1)/x )
- = limx→∞( x/x+1/x )
- = limx→∞( 1+1/x )
- = limx→∞1 + limx→∞(1/x )
- = 1 + limx→∞(1/x )
- = 1 + 0 = 1
- Prove limx→∞(1/x ) = 0
- limx→∞f(x ) = L iff for every ε, there is δ such that x > δ means that | f(x) - L | < ε
- | 1/x | < ε
- |x | > 1/ε
- Suppose I leave Geneseo at 8:00 some morning, driving to New
York City. At the same time Prof. X leaves Toronto driving to
Geneseo. Is there ever a time when I and Prof. X are exactly
the same distance from Geneseo (although in different places)?
- Introduction to derivatives
- Section 3.2
- Limits and derivatives problem set