SUNY Geneseo Department of Computer Science

The Master Method

Return to List of Lectures

Questions?

Analyzing Execution Time and the Master Method

Quicksort

    quicksort( A, first, last )
        if first > last
            p = partition( A, first, last )     // Θ(n)
            quicksort( A, first, p-1 )          // T(n/2)
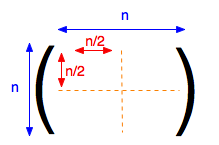
            quicksort( A, p+1, last )           // T(n/2)

• Assume partition runs in Θ(n) time, and divides A exactly in half
• Recurrence
  • T(1) = 1
  • T(n) = 2 T(n/2) + n if n > 1
• Master method
  • a = 2
  • b = 2
  • f(n) = n
  • n^log_ba = n^log₂2 = n
  • f(n) = Θ(n^log_ba) so case 2 applies: T(n) = Θ(nlogn)

Strassen’s algorithm

    strassen( A, B, n )
        if n == 1
            return A[1][1] * B[1][1]
        else
            compute S1 through S10, sums and differences of n/2-by-n/2 matrices
            compute P1 through P7, products of n/2-by-n/2 matrices
            compute C as sums and differences of certain P matrices
            return C

• See book for details
• How Strassen divides matrices

• Matrix addition and subtraction for k-by-k matrices run in Θ(k²) time

        given k-by-k matrices X and Y, with sum to go in Z
        for i = 1 to k
            for j = 1 to k
                Z[i][j] = X[i][j] + Y[i][j]

• So the recursive portion of Strassen’s algorithm runs in time T(n) = 7 T(n/2) + Θ(n²)
• Master method
  • a = 7
  • b = 2
  • f(n) = n²
  • n^log_ba = n^log₂7 ≈ n^2.8
  • f(n) = O( n^log_ba-ε ) so case 1 applies: T(n) = Θ( n^log_ba ) = Θ(n^2.8)

Our kth-smallest algorithm

    kth( k, A, first, last )
        if first == last
            return A[first]
        else
            p = partition( A, first, last )
            if k < p - first + 1
                return kth( k, A, first, p-1 )
            else if k > p - first + 1
                return kth( k - p + first - 1, A, p+1, last )
            else
                return A[p]

• Assume partition takes Θ(n) time, divides array section in half, algorithm never finds p = k - first + 1
• Recurrence
  • T(1) = 1
  • T(n) = T(n/2) + n if n > 1
• Note that only one of the recursive calls gets executed in any invocation of kth, so the recurrence only has 1 T(n/2) in it even though 2 appear textually in the algorithm
• Master method
  • a = 1
  • b = 2
  • f(n) = n
  • n^log_ba = n^log₂1 = 1
  • f(n) = Ω( n^log_ba+ε )
  • a f(n/b) = n/2 ≤ c f(n) = c n for 1/2 ≤ c < 1
  • Third case applies, so T(n) = Θ( f(n) ) = Θ( n )

Naive version of exponentiation

    power( x, n )
        if n == 0
            return 1
        else if n is even
            return power( x, n/2 ) * power( x, n/2 )
        else
            return x * power(x,(n-1)/2) * power(x,(n-1)/2)

• Recurrence
  • T(0) = 1
  • T(n) = 2 T(n/2) + 1 if n > 0
• Master method
  • a = 2
  • b = 2
  • f(n) = 1
  • f(n) = O( n^log_ba-ε ) = O( n^1-ε )
  • First case applies, T(n) = Θ(n^log_ba ) = Θ(n)
• Moral: coding the algorithm naively (namely by calling power more than needed) turned the Θ(logn) time calculated last class into something exponentially worse, and no better than the brute-force algorithm that multiplies n copies of x together

Hand out master method problem set

Next

Introduction to dynamic programming

Read chapter 15 introduction and section 15.1