SUNY Geneseo Department of Computer Science
Introduction to Recurrence Analysis
Thursday, February 14
CSci 242, Spring 2013
Prof. Doug Baldwin
Return to List of Lectures
Previous Lecture
Misc
First hour exam postponed until Thursday Feb. 28
Questions?
Recurrence Relations and Analyzing Execution Time
Example: divide-and-conquer exponentiation
power( x, n )
if n == 0
return 1
else if n is even
temp = power( x, n/2 )
return temp * temp
else
temp = power( x, (n-1)/2 )
return x * temp * temp
- Set up a recurrence relation that describes execution time
- Figure out what parameter determines the time: in this case, n
- In the base case, the algorithm takes constant time—since we only need an asymptotic result, call it 1
- In the recursive case, the algorithm calls itself on n/2 (or floor of n/2, which for asymptotic purposes is n/2), which must take time T(n/2), and does some constant amount of work (multiplying, some comparisons) around the call, which again can be treated as taking 1 unit of time. The total execution time in the recursive case is thus T(n/2) + 1
- Putting the base case and recursive case analyses together (and being a little more precise about the division) gives a recurrence relation
- T(n) = 1 if n = 0
- T(n) = T(⌊n/2⌋) + 1 if n > 0
- Find a closed form
- Tabulate some values of T(n) and see if a pattern emerges
| n |
T(n) |
| 0 |
1 |
| 1 |
T(⌊n/2⌋) + 1 = T(0) + 1 = 2 |
| 2 |
T(⌊2/2⌋) + 1 = T(1) + 1 = 3 |
| 3 |
T(⌊3/2⌋) + 1 = T(1) + 1 = 3 |
| 4 |
T(⌊4/2⌋) + 1 = T(2) + 1 = 4 |
- Generally, T() seems to increase in value at powers of 2, which suggest a log2n term, plus an offset to get the exact values right: T(n) = ⌊log2n⌋ + 2, whenever n ≥ 1.
- Prove the closed form correct
- Induction on n
- Base case: n = 1
- ⌊log2n⌋ + 2 = 0 + 2
- = 2
- = T(1) from definition of T
- Induction hypothesis (strong induction): assume T(n) = ⌊log2n⌋ + 2 whenever n ≤ k ≥ 1.
- Show T(k+1) = ⌊log2(k+1)⌋ + 2
- Case 1: k+1 is odd
- T(k+1) = T( ⌊(k+1)/2⌋ ) + 1 by definition of T and because k+1 > 1
- = ⌊log2( (k+1)/2 )⌋ + 2 + 1 by the induction hypothesis (which can be applied to T( ⌊(k+1)/2⌋ ) because for an odd k+1 > 1, ⌊(k+1)/2⌋ ≤ k)
- = ⌊log2(k+1) - log22⌋ + 3
- = ⌊log2(k+1)⌋ - 1 + 3
- = ⌊log2(k+1)⌋ + 2
- Case 2: k+1 is even
- Exactly the same as above, checking that for even k+1 ≥ 1, ⌊(k+1)/2⌋ ≤ k (we didn’t actually have to do the proof by cases)
A simpler way to find a (asymptotic) closed form: the master method
- a = 1
- b = 2
- f(n) = 1
- So f(n) = Θ( nlogba ) = Θ( nlog21 ) = Θ( n0 ) = Θ( 1 )
- Thus by case 2 T(n) = Θ( nlogba lgn ) = Θ( logn )
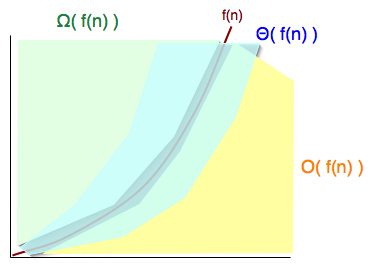
Asymptotic notations
- g(n) = O( f(n) ) means
- There exists c : for all n ≥ n0 : g(n) ≤ c f(n)
- g(n) = Ω( f(n) )
- There exists c : for all n ≥ n0 : g(n) ≥ c f(n)
- g(n) = Θ( f(n) )
- There exists c1 and c2 : for all n ≥ n0 : c1 f(n) ≤ g(n) ≤ c2 f(n)
Next
More execution time analysis
Next Lecture

