SUNY Geneseo Department of Computer Science

Correctness of Loops

Return to List of Lectures

Questions?

Loop Invariants

Note on the sorting algorithm you invented Monday:

    for ( i = 1; i < A.length; i = i + 1 ) {
        for ( j = i; j > 0; j-- ) {
            if ( A[j] < A[j-1] ) {
                k = A[j-1];
                A[j-1] = A[j];
                A[j] = k;
            }
            else {
                break;
            }
        }
    }

• It is actually a classic sorting algorithm, known as "insertion sort"

Correctness of iterative algorithms

• Section 8.2 up through 8.2.3
• Proving iterative algorithms correct
• Three sections
  • Prove that loop will exit
    • Each iteration changes some counter by some minimum non-zero value in direction of exit condition
  • Prove that loop invariant always holds
    • Induction
  • Prove that when loop exits, postconditions hold
    • Use loop invariant, show it produces postcondition at end?
    • Start from facts that
      • Loop's continuation condition is false
      • Invariant still holds
    • Deduce from these (and possibly statements executed after loop) that postconditions hold

Example: prove that insertion sort (in a more concise form) really leaves A in ascending order

    for ( i = 1; i < A.length; i++ ) {
        for ( j = i; j > 0 && A[j] < A[j-1]; j-- ) {
            k = A[j-1];
            A[j-1] = A[j];
            A[j] = k;
        }
    }

• Step 1: prove that "i" loop exits
  • Each iteration reduces distance between i and A.length, the exit condition
• Step 2: prove that "j" loop exits
  • Each iteration reduces distance between j and 0, the exit condition
• Step 3: Prove that loop invariant holds for inner loop
  • Invariant: A[j] through A[i] are in ascending order at beginning of inner loop

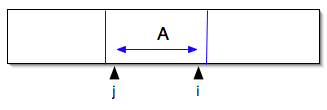
• When loop starts, j = i, A[j..i] only has 1 element, must be in order
• Base case, mini-assignment: work out the induction step

Hand out Problem Set 9

Next

Simple iterative sorting algorithms (no reading)