MATH 380 Conics ala Calculus II

The standard syllabus of Calculus II contains material on the conic sections as the graphs of relations of the form . The curves are given by geometric definitions and these definitions give rise to relations like the one above with conditions on the coefficients. We begin with the parabola, the simplest of these curves to represent.

1. The Parabola

Locus Definition

A parabola is the set of all points equidistant from a given point and a given line not containing the given point.

We will assume that the given point is (0,p) and that the given line is y = -p. This guarantees that (0,0) is a point on the parabola, and indeed a special point. We then simply compute the distances d₁ and d₂ from an arbitrary point to and .

and . (Draw a picture).

We set and square both sides.

.

or .

We will say that the parabola given by is in standard form. There are traditional names for various points and lines connected with this parabola. The given point, (0,p) is called the focus (for reasons which will soon be given). The line y = -p is called the directrix. The line x = 0, which is the y-axis is called the axis of the parabola. The point (0,0) is called the vertex.

Exercise 1. Let p = ¼ and sketch the graphs of the four parabolas given by:

a) b) c) d)

What are the foci, directrices, axes, and vertices of these parabolas?

Note that in all the parabolas in Exercise 1 the axes are parallel to either the x-axis or the y-axis. We can shift any of these parabolas to another position in the plane simply by moving the vertex. Suppose we are given a parabola and want this curve to be translated so that its vertex is at the point (h,k). We replace x by (x – h) and y by (y – k) to yield . Expanding this equation gives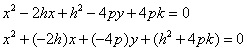

The last line is in the form given at the beginning of this section. If we translate the parabolas given in Exercise 1 so that they have their vertices at (h,k) then the defining algebraic relation has either an x² or a y² term (but not both) and no xy term. They look like one of the following:

or .

Not all parabolas in the x-y plane are of one of these two forms. If the directrix is not parallel to one of the coordinate axes then the equation of the curve is more complicated.

Exercise 2.(*) Let the focus of a parabola be (p,q) and the directrix be the line . Recall from Calculus II the formula for the distance from a point to the line . Well maybe you don’t recall. It’s . Using this formula find the equation of the parabola with the given directrix and focus. You might try the problem with specific numbers for p, q, etc and then try it in full generality. The final result will be rather complex. Write the final result in the form and compute the quantity .

By what we said earlier, the equation should be a parabola with its axis parallel to the y-axis. By completing the square we can put it in standard form and identify the aspects of the curve. The key step is to complete to a square.

We take half of the x coefficient, square it , add and subtract it.

Our original equation becomes:

We can read off the relevant data concerning the parabola.

p = 2.

Vertex (2,-3).

Focus (2,-3+2) = (2,-1)

Axis x = 2

Directrix y = -3 – 2 = -5.

Exercise 3. Complete the square and find all the relevant data for the following parabolas:

a)

b)

c)

The Reflective Property of the Parabola

Imagine that the graph of is actually a mirror and that a light ray inside the parabola is moving parallel to the axis of the parabola. The ray will reflect off the curve and pass through the focus. We will demonstrate this below.

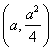The focus of is the point (0,1) and a line parallel to the axis has an equation of the form x = a. This line intersects the parabola at . To show the reflective property we must show that the normal line to the parabola at 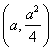bisects the angle formed by the line x = a and the line joining 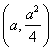and the focus (0,1). The normal line is the line perpendicular to the tangent line. The slope of the tangent line is . (Why?) Thus the slope of the normal line is .

Exercise 4. (**)Using the discussion above show that the normal line bisects the angle joining the line from the focus and the line parallel to the axis. You might try this with a particular value of a first, say a = 2.

2. The Ellipse

Locus Definition

An ellipse is the set of all points the sum of whose distances to two given points is a given quantity.

We will take the two given points to be and . Let the sum of the distances be 2a. Let (x,y) be an arbitrary point on the ellipse. Using the distance formula we have or .
Squaring both sides gives .

Expanding yields . Simplifying we have .

Letting we have

or .

The points (c,0) and (-c,0) are called the foci of the ellipse. We will call the point (0,0) the center of the ellipse. It is analogous to the vertex of the parabola. The quantity 2a is called the major axis. Notice that which means that . We call the quantity 2b the minor axis. The points and are on the ellipse, in fact they are the points where the ellipse intersects the x and the y axes respectively. The length of the line segment connecting (a,0) and (-a,0) is 2a. Thinking of that as the longest “diameter” of the ellipse makes major axis an appropriate term. Why is minor axis appropriate for 2b?

Exercise 5. How is the equation of the ellipse changed if the foci are at ? What happens to the equation if we wish to translate the whole ellipse so that its center is at the point (h,k)?

Exercise 6. Find the equations of the ellipses which have the following given data:

a) Foci (2,2) and (8,2), Minor axis 4.

b) Center (2,-2), Major axis 20, Minor axis 16.

c) Foci (0,0) and (0,-10), Minor axis 2.

Exercise 7. Transform the following equations into standard form and find all the relevant data for the given ellipse:

a)

b)

The Reflective property of the Ellipse

Let P be a point on an ellipse and let A and B be the foci. Then the bisector of the angle is perpendicular to the tangent line at P. Note that this is well known if the ellipse happens to be a circle.

Exercise 8. (**)Choose a non-circular ellipse and a point on that ellipse and demonstrate the reflective property by computation.

3. The Hyperbola

Locus Definition

A hyperbola is the set of all points the difference of whose distances to two given points is a given quantity.

Again we take the given points (also called foci) to be (c,0) and (-c,0). Let 2a be the given difference. The quantity 2a is called the axis, the points the vertices, and (0,0) the center.

The quantity b has an important role with the hyperbola. Suppose that we have the hyperbola . Then the lines are the asymptotes of the hyperbola. The curve approaches these lines as x gets very large.

Exercise 9. Letting . With a derivation similar to that for the ellipse show that the equation of the hyperbola with the given foci and difference is .

Exercise 10. Put the foci at . How does that change the equation in Exercise 7?

Exercise 11. Find the equations of the hyperbolas which have the following given data and find the equations of the asymptotes:

a) Foci (0,0) and (8,0), and one vertex at (2,0).

b) Vertices (1,1) and (1,9) and one focus at (1,10).

Exercise 12. Transform each of the following equations into standard form and then determine the relevant data for the hyperbola:

a)

b)

Exercise 13. (*) What is the reflective property of the hyperbola? Verify this by example.

4. Conics that do not have axes parallel to the x or y axis.

Conic sections in the x-y plane can always be expressed by an equation of the form: . If b = 0, then by completing the square we can determine the nature of the curve. If, however, b ¹ 0, then completing the square will not work. Instead in order to determine the curve we need to rotate the plane since in this case the axis or axes of the curve is not parallel to either the x or y axis. We will assume that the curve is centered on the origin and that if we rotate the plane through a counter-clockwise angle of measure, it will be in a standard position. How does one determine ? The necessary equation is . Then in terms of new axes, and given by , the curve will be in a standard position.

For example, consider the hyperbola given by . In this case a = c = 0, and b = 1. 2 is 90° or p/2 by the above formula. Letting = 45° we have and . Substituting these into the equation xy = 1 yields . We recognize as a hyperbola with its axis along the x-axis.

There is a simple test for the type of curve when b ¹ 0. One computes the quantity (sound familiar) and the sign of this quantity gives us the curve. It is possible with the general equation that we do not have a conic section but instead have lines or points only. For example gives two lines and not a hyperbola. Assuming that we have a conic section the following hold:

If > 0, then the curve is a hyperbola.

If = 0 then the curve is a parabola.

If < 0 ,then the curve is an ellipse.

Exercise 14. Using the discriminant, , determine the nature of the following curves:

a)

b)

c)

Exercise 15. Rotate each of the following to determine a new equation for the conic section:

a)

b)

The transformation given by is a rotation of the xy plane about the origin through an angle of . This transformation leavesthe value of the discriminant unchanged.

Exercise 16. (*) Show that the discriminant is unchanged by the rotation above. Start with a conic - - (you don’t need the other terms) and apply the transformation. Rearrange the terms to yield an equation of the form - - and show that .

Exercise 17. Using the fact from Exercise 16 show that the sign of the discriminant actually does predict the kind of curve. (Hint: What is the discriminant for an ellipse in standard position?)