Quadratic Residues
Theorem
3.1 (page 132)
Let p be an odd prime. Then
1.  ,
,
2. 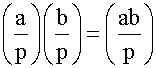 ,
,
3. 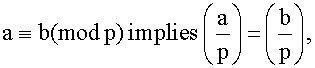
4.
If (a,p) = 1, then 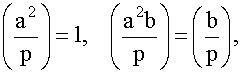
5. 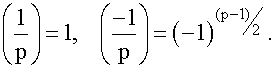
Proof. 1 and 5 were proved on Monday.
2.
Since 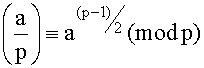 and
and  we have
we have 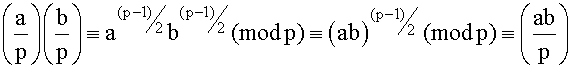 .
.
3. Use part 1 again.
4. 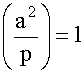 since a2
is a square. Now apply part 2.
since a2
is a square. Now apply part 2.
We
state the next two theorems without proof.
Theorem
3.3 For any odd prime p, 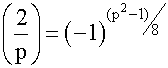 .
.
Theorem
3.4 (page 137)
Gauss’ Law of Quadratic Reciprocity
If p and q are distinct odd primes, then
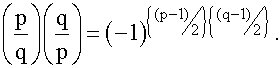
These
theorems allow us to answer the question “Is a a quadratic residue mod p?”
rather easily, without large computations.
Example. Is 7 a quadratic residue mod 59?
Compute 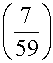 . By Quadratic
Reciprocity we have
. By Quadratic
Reciprocity we have 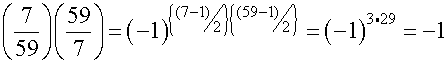 . By reducing mod 7
we have
. By reducing mod 7
we have
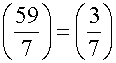 . We apply
reciprocity to
. We apply
reciprocity to ![]() .
.
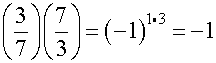 and
and 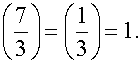
Thus
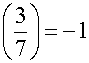 .
.
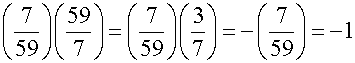 .
.
So  . 7 is a quadratic
residue mod 59.
. 7 is a quadratic
residue mod 59.
Example. Is 30 a square mod 89?
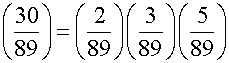
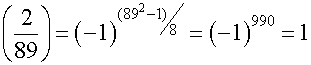 .
.
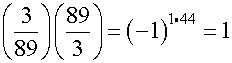 .
. 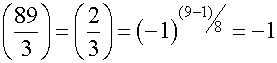 .
.
Thus
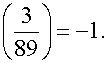

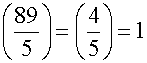 .
.
Thus
we have 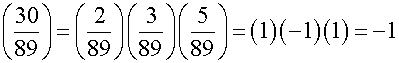 .
.
30
is not a perfect square mod 89.
Now
a harder problem.
Find
all odd primes, p, such that 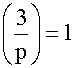 .
.
Let
p be an odd prime, different from 3. Then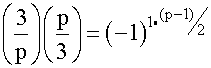 .
.
Since
p is an odd prime, different from 3 we have that ![]() .
.
Case
1: ![]() .
.
In
this case  . Then
. Then 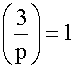 if (p-1)/2 is an even number. This is true if (p-1)/2 = 2k for some
integer k. This reduces to p = 4k+1 or
if (p-1)/2 is an even number. This is true if (p-1)/2 = 2k for some
integer k. This reduces to p = 4k+1 or ![]()
We
now have two congruences to solve simultaneously (using the Chinese Remainder
Theorem):
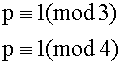
The
solution is ![]()
Case
2: ![]()
In
this case we have shown that 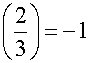 .
.
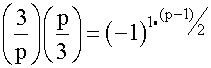 reduces to
reduces to 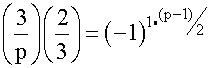 =
=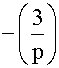 . We now need to have
(p-1)/2 be an odd number. If (p-1)/2 =
2k+1 then p=4k+3 or
. We now need to have
(p-1)/2 be an odd number. If (p-1)/2 =
2k+1 then p=4k+3 or ![]()
The
two congruences to solve in this case are:
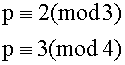
The
only solution is ![]()
Our
final solution is 3 is a quadratic residue mod p for p an odd prime if and only
if p is congruent to either 1 or 11 mod 12.