MATH 301 Logic
Definition 1.2.1. A first-order language L is an infinite collection of distinct symbols, no one of which is properly contained in another, separated into the following categories:
1. Parentheses: ( , ).
2. Connectives: Ú, Ø.
3. Quantifier: ".
4. Variables, one for
each positive integer n: 
.
The set of variable symbols will be denoted by Vars.
5. Equality symbol: =.
6. Constant symbols: Some set of zero or more symbols.
7. Function symbols: For each positive integer n, some set of zero or more n-ary function
symbols.
8. Relation symbols: For each positive integer n, some set of zero or more n-ary relation
symbols.
Definition 1.3.1. If L is a language, a term of L is a nonempty finite string t of symbols from L such that either:
1. t is a variable, or
2. t is a constant symbol, or
3. t
is 
where f is an n-ary function
symbol of L and each of the 
is a term of L.
Definition
1.3.3. If L is a first order language, a formula of L is a nonempty finite string 
of symbols from L such
that either:
1. is 
, where 
and 
are terms of L, or
2. is 
, where R is
an n-ary
relation symbol of L and 
are all terms of L, or
3. is 
, where 
is a formula of L, or
4. is 
, where and 
are formulas of L, or
5. is 
, where v is
a variable and is a formula of L.
The atomic formulas are those given by 1. and 2.
Definition
1.5.1. The language LNT
is 
, where 0 is a constant symbol, S a fixed unary
function symbol, +, ×, and E are binary function symbols, and 
is a binary relation
symbol. This will be referred to as the language of number theory.
Definition
1.5.2. Suppose that v is a
variable and is a formula. We will
say that v is free in if
1. is atomic and v occurs in (is a symbol in) , or
2. is
and v is free in , or
3. is
and v is free in at least one of or , or
4. is
and v is not u and v is free in .
Definition 1.5.3. A sentence in a language L is a formula of L that contains no free variables.
Definition 1.6.1. Fix a language L. An L-Structure U is a nonempty set A, called the universe of U, together with:
1. For each constant symbol c of L, an element 
of A
2. For each n-ary function symbol f of L, a function 
3. For each n-ary relation symbol R
of L, an n-ary
relation 
on A (i.e., a
subset of 
).
Definition 1.7.1. If U is an L-structure, a variable assignment function into U is a function s that assigns to each variable an element of the universe A. So a variable assignment function into U is any function with domain Vars and codomain A.
Definition
1.7.2. If s is a variable assignment function into
U
and x is a variable and aÎA, then 
is the variable
assignment function into U defined as follows:
We call the
function an x-modification
of the assignment function s.
Definition
1.7.3. Suppose that U
is an L-Structure and s is a variable
assignment function into U. The function 
, called the term
assignment function generated by s,
is the function with domain consisting of the set of L-terms and codomain A
defined recursively as follows:
1. It t is a
variable, 
2. If t is a constant
symbol c, then 
3. If t is , then 
Definition
1.7.4. Suppose that U is an L-structure, is an L-formula, and 
is a variable
assignment function. We will say that U satisfies with assignment s, and
write 
╞
, in the following circumstances:
1. If is and 
is the same element of
the universe A as 
, or
2. If is 
and 
, or
3. If is and U
(where 
means ‘does not satisfy”), or
4. If is and U╞
or U╞
(or both), or
5. If is 
and for each element a of A, U╞
.
If 
is a set of
L-formulas, we say that U satisfies with assignment s, and write U╞
if for each 
, U╞
Definition 1.7.9. If
is a formula in the language L and U is an L-structure, we say that U is a model of , and write U╞, if and only if U╞ for every assignment function s. If 
is a set of L-formulas,
we will say that U models
, and write U╞, if and only if U╞ for each 
.
Definition 1.8.1. Suppose that u is a term, x is a
variable, and t is a term. We define
the term 
(read “u with x replaces by t”) as
follows:
1. If u is a variable
not equal to x, then is u.
2. If u is x, then is t.
3. If u is a constant
symbol, then is u.
4. If u is 
, where f is an n-ary function
symbol and the ui
are terms, then
is 
.
Definition 1.8.2. Suppose
that is an L-formula, t is a term, and x is a variable.We define the formula 
(read “ with x replaced by
t”) as follows:
1. If is 
, then is 
.
2. If is 
, then is 
.
2. If is 
, then is 
.
4. If is , then is 
.
5. If is 
, then
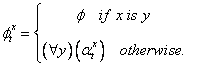
Definition 1.8.3. Suppose that is an L-formula, t is a term, and x is a variable. We say that t
is substitutable for x in
if
1. is atomic, or
2. is and t is substitutable for x in , or
3. is and t is substitutable for x in both and , or
4. is and either
(a) x is not free in , or
(b) y does not occur
in t and t is substitutable for x
in .
Definition 1.9.1. Suppose that 
and are sets of
L-formulas. We will say that logically implies and write ╞ if for every L-structure U,
if U╞, then U╞.
Definition 1.9.2. An L-formula is said to be valid if 
╞, in other words, if is true in every
L-structure with every assignment function s.
In this case we will write ╞.
Definition 2.2.1. Suppose that 
is a collection of
L-formulas and D is a finite sequence
of L-formulas. We will say that D is a deduction from if for each i, 
, either
1. 
(
is a logical axiom), or
2. 
( is a nonlogical axiom), or
3. There is a rule of inference 
such that 
.
If there is a deduction from , the last line of which is the formula , we will call this a deduction
from of , and write ├ .
Definition 2.4.1. Suppose that 
is a set of
propositional formulas and 
is a propositional
formula. We will say that is a propositional
consequence of if every truth
assignment that makes each propositional formula in true also makes true. Notice that is a tautology if and
only if is a propositional
consequence of .
Definition 2.4.3. Suppose that is a set of L-formulas and is an L-formula. We
will say that is a propositional consequence
of
if is a propositional
consequence of , where and are the results of
applying the procedure on the preceding page (page 59) uniformly to and to all the
formulas in .
Definition 2.4.5. If
is a finite set of
L-formulas, is an L-formula, and is a propositional
consequence of , then 
is a rule of inference of type (PC).
Definition 2.4.6. Suppose that the variable x is not free in the formula 
. Then both of the following are rules of inference of type (QR):
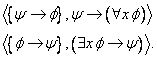
Definition 3.1.1. A
deductive system consisting of a collection of logical axioms 
and a collection of
rules of inference is said to be complete
if for every set of nonlogical axioms and every L-formula ,
If
╞ , then ├ .
Definition 3.2.1. Let
be a collection of
L-formulas. We will say that is inconsistent if there is a deduction
form of 
. We say that is consistent if it is
not inconsistent.
Definition 3.3.4. If U
is an L-structure, we define the theory
of U to be Th(U) = {
is an L-formula and U╞}. If U and B are L-structures such that Th(U) = Th(B) , then we say that U and B are elementarily
equivalent , and write U
.
If
, we say that U
is a model of arithmetic.
Definition 3.4.1. If
U and B are two L-structures, we will say that U is a substructure of B, and write 
, if:
1. 
, where A
and B are the universes of the given
structures.
2. For every constant symbol c, 
.
3. For every n-ary relation symbol R,
4. For every n-ary function symbol f,
In other words, for
every n-ary
function symbol f and every 
, 
(This is called the restriction of the function 
to the set 
Definition 3.4.4. Suppose that U and B are L-structures and . We say that U
is an elementary substructure of B (equivalently, B is an elementary extension
of U), and write 
, if for every 
and every L-formula ,
U╞
if and only if B╞.