MATH 222 – Exercises on Exponential Models Solutions at the end.

Names__________________________________________________

1. A researcher starts two bacteria cultures at the same time using the same strain of bacteria in each case. The first culture reaches 10,000 bacteria in four hours. The second culture starts with twice as many bacteria and reaches 10,000 in three hours. Assuming exponential growth with the same relative growth constant what are the initial populations of the two cultures?

2. Two ponds are stocked with fish, each pond with a different type. The first pond begins with 50 fish while the second begins with 200. One year later the first pond has 450 fish while the second has 1400. How long does it take the first pond to catch up with the second pond in population?

3. Using very careful measurements of the radioactive element Patakium, a researcher finds that 2% of his sample decays in 3 hours. Find the half-life of Patakium.

4. A population obeying the logistic growth equation has an initial population of 40 and a carrying capacity of 200. After one month the population has grown to 60.

a) Find P(t) for this population.

b) Suppose that 10 individuals are removed from the population when it is at 120. How long does it take the population to return to the level of 120? Repeat the computation for 100 and for 80.

Solutions:

1. We write equations for each population: . We also know that P₁(4) = 10,000 and P₂(3) = 10,000. Thus we have . Setting the outer two equal and dividing out P₀ yields . Divide both sides by e^3r to obtain e^r = 2. Thus r = ln(2). From that we compute P₁(4) again to get 10,000 = P₀e^4ln(2) = P₀(16). thus P₀ = 625. the initial populations are 625 and 1250.

2. We write equations and find the values of r and s. Since P₁(1)=450 we have 450 = 50e^r or r = ln(9). We also have 1400 = 200e^s or s = ln(7). It now remains to solve for t in P₁(t) = P₂(t), or . Divide both sides by 50 and then take the natural logarithm of both sides to yield ln(9)t = ln(4) + ln(7)t. Solving for t gives

3. Recall that the half-life T is related to the constant r in N(t)=N₀e^rt by the formula r = -ln2/T. We can thus find T easily if we know r. We have (.98)N₀ = N₀e^3r. Divide by N₀ and takes natural logs to give r = ln(.98)/3. Since T = -ln2/r we have T = (-ln2)/(ln(.98)/3) = -3ln(2)/ln(.98) = 102.93.

4. We begin with K = 200 and N₀ = 40. This gives the constant A the value (200-40)/40 = 4. Thus we have . Since P(1) = 60, we can solve for r to get .

a) .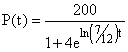

b) We solve the two equations P(t₁) = 120 and P(t₂) = 110 to get t₁ = 3.32425 and t₂=2.94429. Subtracting t₂ from t₁ gives the time it takes the population to grow from 110 to 120, which is .37996 months. Setting P(t₁) = 100 and P(t₂) = 90 we get the time difference to be .37231 and setting P(t₁) = 80 and P(t₂) = 700 we get the time difference to be .396244.