MATH 222 - Logistic Population Growth

If we adjust our model for exponential population growth so that the growth of the population slows down as the population approaches a certain value we develop a more realistic model called Logistic Growth. Our original equation was . To this we add a term to get the equation where M is the ideal population for the particular environment. M is usually called the “carrying capacity”. We add the initial condition N(0)=N₀. To solve the equation we “separate the variables” N and t.

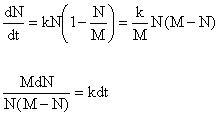
We need to simplify the left hand side by the method of “partial fractions”’.

(Check this equation.)

Thus

and .

Setting these equal we have ln(N)-ln(M-N)=kt+C, which yields

Using N(0)=N₀ we have

In full detail our solution looks like this: 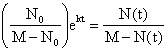. Let Then our equation becomes: .

Solving for N(t) yields

Then we have

Finally, let . Divide the numerator and denominator by Ae^kt. Then we have .

Example 1. Suppose that N₀ = 10, M = 100, and N(1) = 20.

A=10/(100-10)=10/90=1/9. B = 9. The solution up to this point is

Using the last piece of information we have We solve for k:

We have k = -ln(4/9) = ln(9/4).

The final solution is .

The graph of the solution is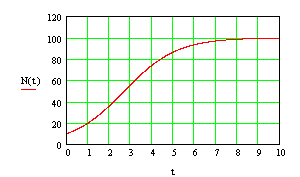

Notice that the horizontal line N(t)=100 is a horizontal asymptote.

Exercise1. Find the solution N(t) for N₀ = 5, M = 100, and N(1) = 15. Graph the solution on the calculator.

Exercise 2. Find the solution N(t) for N₀ = 25, M = 1000, and N(2) = 60. Find the value of t at which N(t) = 500 = M/2.

Exercise 3. Find N(t) if N₀ = 10, M = 50, and N(2) = 20. For what t does N(t)=45?

Graph the solution. For what value of t is N(t) rising the most steeply? What is N equal to at that value of t?

Exercise 4. Suppose that a population starts at a level above the carrying capacity. What does the model predict? Let N₀ = 150 and M = 100. Also suppose that N(1)=125. Find N(t) and graph the result.